Polycrystal Initial Conditions
Polycrystal Initial Conditions can be created in a few ways. They can be read from a file, generated with Voronoi Tesselation of a set of points, or placed in some regular crystal pattern such as hex or circles. In any case, it is advantageous to simulate such a system with a reduced number of order parameters for efficiency, which requires the use of the Grain Tracker. The trickiest part of running a reduced order parameter model however, is the initial assignment of order parameters to grains. This process is akin to solving a graph coloring. Fortunately, the order parameter assignment process has been taken care of for you. Each polycrystal initial condition should simply extend the PolycrystalUserObjectBase class.
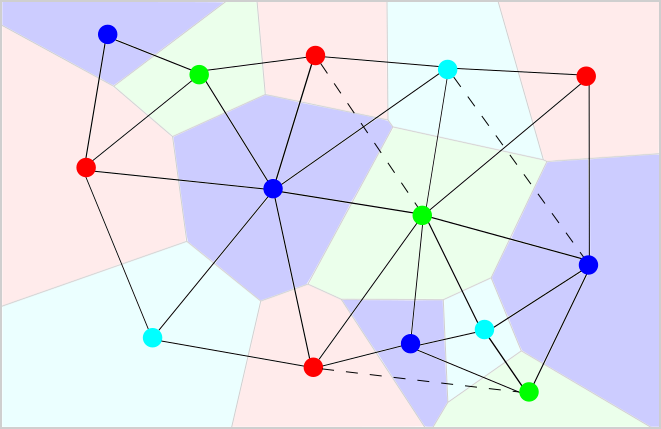
Grain structure with associated neighbor graph overlaid.
Extensions of this class must begin by providing reporting the number of grains in the initial condition.
virtual unsigned int getNumGrains() const = 0;
Additionally, the developer must provide an implementation for reporting the grain(s) at every point in the domain:
virtual void getGrainsBasedOnPoint(const Point & point,
std::vector<unsigned int> & grains) const = 0;
Finally, a method to report the variable value of the current order parameter at a point must be provided. This method is called after order parameters have been assigned to all grains.
virtual Real getVariableValue(unsigned int op_index, const Point & p) const = 0;
The object uses these implementations to build a grain adjacency graph that can be feed to a stochastic or deterministic graph coloring algorithm. MOOSE defaults to using one of the built-in high performance coloring algorithms from the PETSc package. However, a simple backtracking algorithm is also included which works reasonably well on smaller to mid-sized problems.
The centroids of grains can be randomly generated or read from a file. The use of Maximal Poisson-Disk Sampling (MPS) to generate grain centroids is described in MPS.
See:
(moose/modules/phase_field/include/userobjects/PolycrystalUserObjectBase.h)
// This file is part of the MOOSE framework
// https://www.mooseframework.org
//
// All rights reserved, see COPYRIGHT for full restrictions
// https://github.com/idaholab/moose/blob/master/COPYRIGHT
//
// Licensed under LGPL 2.1, please see LICENSE for details
// https://www.gnu.org/licenses/lgpl-2.1.html
#pragma once
#include "DenseMatrix.h"
#include "FeatureFloodCount.h"
// Forward Declarations
/**
* This object provides the base capability for creating proper polycrystal ICs. It is
* able to discover the grain structure to provide information about neighboring grains
* so that they will not be assigned the same order parameters with a reduced set of variables.
*/
class PolycrystalUserObjectBase : public FeatureFloodCount
{
public:
static InputParameters validParams();
PolycrystalUserObjectBase(const InputParameters & parameters);
/**
* This callback is triggered after the object is initialized and may be optionally
* overridden to do precompute the element to grain identifiers ahead of time.
*/
virtual void precomputeGrainStructure() {}
/**
* Method for retrieving active grain IDs based on some point in the mesh. Typically these
* are element centroids or nodes depending on the basis functions being initialized. ICs that
* have fixed resolution data (i.e. experimental datasets) may choose to implement
* the element based method as well for added convenience.
*/
virtual void getGrainsBasedOnPoint(const Point & point,
std::vector<unsigned int> & grains) const = 0;
/**
* This method may be defined in addition to the point based initialization to speed up lookups.
* It returns grain IDs based on the current element. Note: If your simulation contains adaptivity
* the point based method may be used to retrieve grain information as well as this method.
*/
virtual void getGrainsBasedOnElem(const Elem & elem, std::vector<unsigned int> & grains) const
{
getGrainsBasedOnPoint(elem.vertex_average(), grains);
}
/**
* Must be overridden by the deriving class to provide the number of grains in the polycrystal
* structure.
*/
virtual unsigned int getNumGrains() const = 0;
/**
* Returns the variable value for a given op_index and mesh point. This is the method used by the
* initial condition after the Polycrystal grain structure has be setup. Those grains are
* then distributed to the typically smaller number of order parameters by this class.
* This method is then used to return those values but it may be overridden in a derived class.
*/
virtual Real getVariableValue(unsigned int op_index, const Point & p) const = 0;
/**
* Similarly to the getVariableValue method, this method also returns values but may be optimized
* for returning nodal values.
*/
virtual Real getNodalVariableValue(unsigned int op_index, const Node & n) const
{
return getVariableValue(op_index, static_cast<const Point &>(n));
}
/* Returns all available coloring algorithms as an enumeration type for input files.
*/
static MooseEnum coloringAlgorithms();
/**
* Returns corresponding descriptions of available coloring algorithms.
*/
static std::string coloringAlgorithmDescriptions();
/**
* UserObject interface overrides. Derived classes should _not_ override any of these methods.
*/
virtual void initialSetup() override;
virtual void initialize() override;
virtual void execute() override;
virtual void finalize() override;
protected:
virtual bool areFeaturesMergeable(const FeatureData & f1, const FeatureData & f2) const override;
virtual bool isNewFeatureOrConnectedRegion(const DofObject * dof_object,
std::size_t & current_index,
FeatureData *& feature,
Status & status,
unsigned int & new_id) override;
virtual void prepareDataForTransfer() override;
virtual void mergeSets() override;
virtual processor_id_type numberOfDistributedMergeHelpers() const override;
virtual void restoreOriginalDataStructures(std::vector<std::list<FeatureData>> & orig) override;
/**
* Builds a dense adjacency matrix based on the discovery of grain neighbors and halos
* surrounding each grain.
*/
void buildGrainAdjacencyMatrix();
/**
* Method that runs a coloring algorithm to assign OPs to grains.
*/
void assignOpsToGrains();
/**
* Built-in simple "back-tracking" algorithm to assign colors to a graph.
*/
bool colorGraph(unsigned int vertex);
/**
* Helper method for the back-tracking graph coloring algorithm.
*/
bool isGraphValid(unsigned int vertex, unsigned int color);
/**
* Prints out the adjacency matrix in a nicely spaced integer format.
*/
void printGrainAdjacencyMatrix() const;
/*************************************************
*************** Data Structures *****************
************************************************/
/// The dense adjacency matrix
std::unique_ptr<DenseMatrix<Real>> _adjacency_matrix;
/// mesh dimension
const unsigned int _dim;
/// The maximum number of order parameters (colors) available to assign to the grain structure
const unsigned int _op_num;
/// A map of the grain_id to op
std::map<unsigned int, unsigned int> _grain_to_op;
/// The selected graph coloring algorithm used by this object
const MooseEnum _coloring_algorithm;
/// A Boolean indicating whether the object has assigned colors to grains (internal use)
bool _colors_assigned;
/// A user controllable Boolean which can be used to print the adjacency matrix to the console
const bool _output_adjacency_matrix;
/// Used to indicate an invalid coloring for the built-in back-tracking algorithm
static const unsigned int INVALID_COLOR;
/// Used to hold the thickness of the halo that should be constructed for detecting adjacency
static const unsigned int HALO_THICKNESS;
private:
/// The number of chunks (for merging the features together)
processor_id_type _num_chunks;
/// A vector indicating which op is assigned to each grain (by index of the grain)
std::vector<unsigned int> _grain_idx_to_op;
/// Temporary storage area for current grains at a point to avoid memory churn
std::vector<unsigned int> _prealloc_tmp_grains;
std::map<dof_id_type, std::vector<unsigned int>> _entity_to_grain_cache;
};
(moose/modules/phase_field/include/userobjects/PolycrystalUserObjectBase.h)
// This file is part of the MOOSE framework
// https://www.mooseframework.org
//
// All rights reserved, see COPYRIGHT for full restrictions
// https://github.com/idaholab/moose/blob/master/COPYRIGHT
//
// Licensed under LGPL 2.1, please see LICENSE for details
// https://www.gnu.org/licenses/lgpl-2.1.html
#pragma once
#include "DenseMatrix.h"
#include "FeatureFloodCount.h"
// Forward Declarations
/**
* This object provides the base capability for creating proper polycrystal ICs. It is
* able to discover the grain structure to provide information about neighboring grains
* so that they will not be assigned the same order parameters with a reduced set of variables.
*/
class PolycrystalUserObjectBase : public FeatureFloodCount
{
public:
static InputParameters validParams();
PolycrystalUserObjectBase(const InputParameters & parameters);
/**
* This callback is triggered after the object is initialized and may be optionally
* overridden to do precompute the element to grain identifiers ahead of time.
*/
virtual void precomputeGrainStructure() {}
/**
* Method for retrieving active grain IDs based on some point in the mesh. Typically these
* are element centroids or nodes depending on the basis functions being initialized. ICs that
* have fixed resolution data (i.e. experimental datasets) may choose to implement
* the element based method as well for added convenience.
*/
virtual void getGrainsBasedOnPoint(const Point & point,
std::vector<unsigned int> & grains) const = 0;
/**
* This method may be defined in addition to the point based initialization to speed up lookups.
* It returns grain IDs based on the current element. Note: If your simulation contains adaptivity
* the point based method may be used to retrieve grain information as well as this method.
*/
virtual void getGrainsBasedOnElem(const Elem & elem, std::vector<unsigned int> & grains) const
{
getGrainsBasedOnPoint(elem.vertex_average(), grains);
}
/**
* Must be overridden by the deriving class to provide the number of grains in the polycrystal
* structure.
*/
virtual unsigned int getNumGrains() const = 0;
/**
* Returns the variable value for a given op_index and mesh point. This is the method used by the
* initial condition after the Polycrystal grain structure has be setup. Those grains are
* then distributed to the typically smaller number of order parameters by this class.
* This method is then used to return those values but it may be overridden in a derived class.
*/
virtual Real getVariableValue(unsigned int op_index, const Point & p) const = 0;
/**
* Similarly to the getVariableValue method, this method also returns values but may be optimized
* for returning nodal values.
*/
virtual Real getNodalVariableValue(unsigned int op_index, const Node & n) const
{
return getVariableValue(op_index, static_cast<const Point &>(n));
}
/* Returns all available coloring algorithms as an enumeration type for input files.
*/
static MooseEnum coloringAlgorithms();
/**
* Returns corresponding descriptions of available coloring algorithms.
*/
static std::string coloringAlgorithmDescriptions();
/**
* UserObject interface overrides. Derived classes should _not_ override any of these methods.
*/
virtual void initialSetup() override;
virtual void initialize() override;
virtual void execute() override;
virtual void finalize() override;
protected:
virtual bool areFeaturesMergeable(const FeatureData & f1, const FeatureData & f2) const override;
virtual bool isNewFeatureOrConnectedRegion(const DofObject * dof_object,
std::size_t & current_index,
FeatureData *& feature,
Status & status,
unsigned int & new_id) override;
virtual void prepareDataForTransfer() override;
virtual void mergeSets() override;
virtual processor_id_type numberOfDistributedMergeHelpers() const override;
virtual void restoreOriginalDataStructures(std::vector<std::list<FeatureData>> & orig) override;
/**
* Builds a dense adjacency matrix based on the discovery of grain neighbors and halos
* surrounding each grain.
*/
void buildGrainAdjacencyMatrix();
/**
* Method that runs a coloring algorithm to assign OPs to grains.
*/
void assignOpsToGrains();
/**
* Built-in simple "back-tracking" algorithm to assign colors to a graph.
*/
bool colorGraph(unsigned int vertex);
/**
* Helper method for the back-tracking graph coloring algorithm.
*/
bool isGraphValid(unsigned int vertex, unsigned int color);
/**
* Prints out the adjacency matrix in a nicely spaced integer format.
*/
void printGrainAdjacencyMatrix() const;
/*************************************************
*************** Data Structures *****************
************************************************/
/// The dense adjacency matrix
std::unique_ptr<DenseMatrix<Real>> _adjacency_matrix;
/// mesh dimension
const unsigned int _dim;
/// The maximum number of order parameters (colors) available to assign to the grain structure
const unsigned int _op_num;
/// A map of the grain_id to op
std::map<unsigned int, unsigned int> _grain_to_op;
/// The selected graph coloring algorithm used by this object
const MooseEnum _coloring_algorithm;
/// A Boolean indicating whether the object has assigned colors to grains (internal use)
bool _colors_assigned;
/// A user controllable Boolean which can be used to print the adjacency matrix to the console
const bool _output_adjacency_matrix;
/// Used to indicate an invalid coloring for the built-in back-tracking algorithm
static const unsigned int INVALID_COLOR;
/// Used to hold the thickness of the halo that should be constructed for detecting adjacency
static const unsigned int HALO_THICKNESS;
private:
/// The number of chunks (for merging the features together)
processor_id_type _num_chunks;
/// A vector indicating which op is assigned to each grain (by index of the grain)
std::vector<unsigned int> _grain_idx_to_op;
/// Temporary storage area for current grains at a point to avoid memory churn
std::vector<unsigned int> _prealloc_tmp_grains;
std::map<dof_id_type, std::vector<unsigned int>> _entity_to_grain_cache;
};
(moose/modules/phase_field/include/userobjects/PolycrystalUserObjectBase.h)
// This file is part of the MOOSE framework
// https://www.mooseframework.org
//
// All rights reserved, see COPYRIGHT for full restrictions
// https://github.com/idaholab/moose/blob/master/COPYRIGHT
//
// Licensed under LGPL 2.1, please see LICENSE for details
// https://www.gnu.org/licenses/lgpl-2.1.html
#pragma once
#include "DenseMatrix.h"
#include "FeatureFloodCount.h"
// Forward Declarations
/**
* This object provides the base capability for creating proper polycrystal ICs. It is
* able to discover the grain structure to provide information about neighboring grains
* so that they will not be assigned the same order parameters with a reduced set of variables.
*/
class PolycrystalUserObjectBase : public FeatureFloodCount
{
public:
static InputParameters validParams();
PolycrystalUserObjectBase(const InputParameters & parameters);
/**
* This callback is triggered after the object is initialized and may be optionally
* overridden to do precompute the element to grain identifiers ahead of time.
*/
virtual void precomputeGrainStructure() {}
/**
* Method for retrieving active grain IDs based on some point in the mesh. Typically these
* are element centroids or nodes depending on the basis functions being initialized. ICs that
* have fixed resolution data (i.e. experimental datasets) may choose to implement
* the element based method as well for added convenience.
*/
virtual void getGrainsBasedOnPoint(const Point & point,
std::vector<unsigned int> & grains) const = 0;
/**
* This method may be defined in addition to the point based initialization to speed up lookups.
* It returns grain IDs based on the current element. Note: If your simulation contains adaptivity
* the point based method may be used to retrieve grain information as well as this method.
*/
virtual void getGrainsBasedOnElem(const Elem & elem, std::vector<unsigned int> & grains) const
{
getGrainsBasedOnPoint(elem.vertex_average(), grains);
}
/**
* Must be overridden by the deriving class to provide the number of grains in the polycrystal
* structure.
*/
virtual unsigned int getNumGrains() const = 0;
/**
* Returns the variable value for a given op_index and mesh point. This is the method used by the
* initial condition after the Polycrystal grain structure has be setup. Those grains are
* then distributed to the typically smaller number of order parameters by this class.
* This method is then used to return those values but it may be overridden in a derived class.
*/
virtual Real getVariableValue(unsigned int op_index, const Point & p) const = 0;
/**
* Similarly to the getVariableValue method, this method also returns values but may be optimized
* for returning nodal values.
*/
virtual Real getNodalVariableValue(unsigned int op_index, const Node & n) const
{
return getVariableValue(op_index, static_cast<const Point &>(n));
}
/* Returns all available coloring algorithms as an enumeration type for input files.
*/
static MooseEnum coloringAlgorithms();
/**
* Returns corresponding descriptions of available coloring algorithms.
*/
static std::string coloringAlgorithmDescriptions();
/**
* UserObject interface overrides. Derived classes should _not_ override any of these methods.
*/
virtual void initialSetup() override;
virtual void initialize() override;
virtual void execute() override;
virtual void finalize() override;
protected:
virtual bool areFeaturesMergeable(const FeatureData & f1, const FeatureData & f2) const override;
virtual bool isNewFeatureOrConnectedRegion(const DofObject * dof_object,
std::size_t & current_index,
FeatureData *& feature,
Status & status,
unsigned int & new_id) override;
virtual void prepareDataForTransfer() override;
virtual void mergeSets() override;
virtual processor_id_type numberOfDistributedMergeHelpers() const override;
virtual void restoreOriginalDataStructures(std::vector<std::list<FeatureData>> & orig) override;
/**
* Builds a dense adjacency matrix based on the discovery of grain neighbors and halos
* surrounding each grain.
*/
void buildGrainAdjacencyMatrix();
/**
* Method that runs a coloring algorithm to assign OPs to grains.
*/
void assignOpsToGrains();
/**
* Built-in simple "back-tracking" algorithm to assign colors to a graph.
*/
bool colorGraph(unsigned int vertex);
/**
* Helper method for the back-tracking graph coloring algorithm.
*/
bool isGraphValid(unsigned int vertex, unsigned int color);
/**
* Prints out the adjacency matrix in a nicely spaced integer format.
*/
void printGrainAdjacencyMatrix() const;
/*************************************************
*************** Data Structures *****************
************************************************/
/// The dense adjacency matrix
std::unique_ptr<DenseMatrix<Real>> _adjacency_matrix;
/// mesh dimension
const unsigned int _dim;
/// The maximum number of order parameters (colors) available to assign to the grain structure
const unsigned int _op_num;
/// A map of the grain_id to op
std::map<unsigned int, unsigned int> _grain_to_op;
/// The selected graph coloring algorithm used by this object
const MooseEnum _coloring_algorithm;
/// A Boolean indicating whether the object has assigned colors to grains (internal use)
bool _colors_assigned;
/// A user controllable Boolean which can be used to print the adjacency matrix to the console
const bool _output_adjacency_matrix;
/// Used to indicate an invalid coloring for the built-in back-tracking algorithm
static const unsigned int INVALID_COLOR;
/// Used to hold the thickness of the halo that should be constructed for detecting adjacency
static const unsigned int HALO_THICKNESS;
private:
/// The number of chunks (for merging the features together)
processor_id_type _num_chunks;
/// A vector indicating which op is assigned to each grain (by index of the grain)
std::vector<unsigned int> _grain_idx_to_op;
/// Temporary storage area for current grains at a point to avoid memory churn
std::vector<unsigned int> _prealloc_tmp_grains;
std::map<dof_id_type, std::vector<unsigned int>> _entity_to_grain_cache;
};