List of tutorials
All tutorials are written assuming that you are reasonably familiar with MOOSE. If you find most of the tutorials difficult to follow, please refer to the official MOOSE website for learning resources.
Tutorial 2: Mode-I crack propagation
In this tutorial, we will set up the model for Mode-I crack propagation.
The geometry and boundary conditions are the same as those in Tutorial 1.
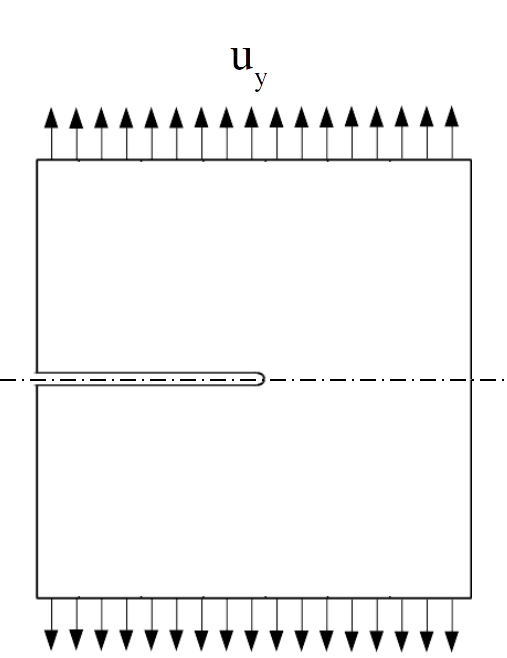
Figure 1: Geometry and boundary conditions of the Mode-I crack propagation problem.
At each time step, the alternative minimization scheme first solves the displacements with a fixed phase-field, then solves the phase-field with the updated displacements. This scheme is realized using MOOSE's MultiApp system. We will set up two input files. One for the displacement subproblem, and the other one for the phase-field subproblem.
elasticity.i: The displacement subproblem
First, we set up the displacement subproblem as our main app. Two additional global expressions are defined at the top of the input file:
Gc = 2.7
l = 0.02
The mesh is locally refined using initial adaptivity:
[Adaptivity]
marker = marker
initial_marker = marker
initial_steps = 2
stop_time = 0
max_h_level = 2
[Markers]
[marker]
type = BoxMarker
bottom_left = '0.4 0 0'
top_right = '1 0.05 0'
outside = DO_NOTHING
inside = REFINE
[]
[]
[]
The quadratic degradation function is defined as
[Materials]
[degradation]
type = PowerDegradationFunction
property_name = g
expression = (1-d)^p*(1-eta)+eta
phase_field = d
parameter_names = 'p eta '
parameter_values = '2 1e-6'
[]
[]
fracture.i: The phase-field subproblem
Next, we set up the phase-field subproblem as our sub app. The sub app uses the same mesh as the main app. The equation we want to solve is
on the inactive set. The (local part of the) free energy, i.e. the term in the paranthesis, is defined using an ADDerivativeParsedMaterial:
[Materials]
[psi]
type = ADDerivativeParsedMaterial
property_name = psi
expression = 'alpha*Gc/c0/l+g*psie_active'
coupled_variables = 'd psie_active'
material_property_names = 'alpha(d) g(d) Gc c0 l'
derivative_order = 1
[]
[]
With the definition of local free energy psi, the following kernels are used to construct the equation:
[Kernels]
[diff]
type = ADPFFDiffusion
variable = d
fracture_toughness = Gc
regularization_length = l
normalization_constant = c0
[]
[source]
type = ADPFFSource
variable = d
free_energy = psi
[]
[]
The bound constraints on the active set is defined using
[Bounds]
[irreversibility]
type = VariableOldValueBounds
variable = bounds_dummy
bounded_variable = d
bound_type = lower
[]
[upper]
type = ConstantBounds
variable = bounds_dummy
bounded_variable = d
bound_type = upper
bound_value = 1
[]
[]
Transferring information between the main and the sub app
The displacement subproblem need to know the solution of the phase-field subproblem, and the phase-field subproblem need to know the active elastic energy psie_active. Therefore, some transfer of information between the two apps must exist.
To do that, we first let the displacement subproblem (the main app) be aware of its subapp by adding the following section to elasticity.i:
[MultiApps]
[fracture]
type = TransientMultiApp
input_files = fracture.i
cli_args = 'Gc=${Gc};l=${l}'
execute_on = 'TIMESTEP_END'
[]
[]
The cli_args makes sure and are consistent across the two apps. The execute_on flag tells the main app to execute the sub app at the end of the time step (after the displacements are solved).
Next, we set up the appropriate transfer:
[Transfers]
[from_d]
type = MultiAppCopyTransfer
from_multi_app = 'fracture'
variable = d
source_variable = d
[]
[to_psie_active]
type = MultiAppCopyTransfer
to_multi_app = 'fracture'
variable = psie_active
source_variable = psie_active
[]
[]
The phase-field is retrieved from the sub app, and the main app sends the active elastic energy to the sub app.
The alternating minimization scheme
Now that we have set up the displacement subproblem, the phase-field subproblem, and the transfers between them, we are now in good shape to set up the alternating minimization scheme.
To do so, we rely on MOOSE's Picard iteration. In essence, a Picard solve iterates between the main app and the sub app(s) until the solution in the main app no longer changes between Picard iterations. We add the following parameters to the Executioner section to enable Picard iteration:
E = 2.1e5
nu = 0.3
K = '${fparse E/3/(1-2*nu)}'
G = '${fparse E/2/(1+nu)}'
Gc = 2.7
l = 0.02
[MultiApps]
[fracture]
type = TransientMultiApp
input_files = fracture.i
cli_args = 'Gc=${Gc};l=${l}'
execute_on = 'TIMESTEP_END'
[]
[]
[Transfers]
[from_d]
type = MultiAppCopyTransfer
from_multi_app = 'fracture'
variable = d
source_variable = d
[]
[to_psie_active]
type = MultiAppCopyTransfer
to_multi_app = 'fracture'
variable = psie_active
source_variable = psie_active
[]
[]
[GlobalParams]
displacements = 'disp_x disp_y'
[]
[Mesh]
[gen]
type = GeneratedMeshGenerator
dim = 2
nx = 30
ny = 15
ymax = 0.5
[]
[noncrack]
type = BoundingBoxNodeSetGenerator
input = gen
new_boundary = noncrack
bottom_left = '0.5 0 0'
top_right = '1 0 0'
[]
construct_side_list_from_node_list = true
[]
[Adaptivity]
marker = marker
initial_marker = marker
initial_steps = 2
stop_time = 0
max_h_level = 2
[Markers]
[marker]
type = BoxMarker
bottom_left = '0.4 0 0'
top_right = '1 0.05 0'
outside = DO_NOTHING
inside = REFINE
[]
[]
[]
[Variables]
[disp_x]
[]
[disp_y]
[]
[]
[AuxVariables]
[fy]
[]
[d]
[]
[]
[Kernels]
[solid_x]
type = ADStressDivergenceTensors
variable = disp_x
component = 0
[]
[solid_y]
type = ADStressDivergenceTensors
variable = disp_y
component = 1
save_in = fy
[]
[]
[BCs]
[ydisp]
type = FunctionDirichletBC
variable = disp_y
boundary = top
function = 't'
[]
[yfix]
type = DirichletBC
variable = disp_y
boundary = noncrack
value = 0
[]
[xfix]
type = DirichletBC
variable = disp_x
boundary = top
value = 0
[]
[]
[Materials]
[bulk]
type = ADGenericConstantMaterial
prop_names = 'K G'
prop_values = '${K} ${G}'
[]
[degradation]
type = PowerDegradationFunction
property_name = g
expression = (1-d)^p*(1-eta)+eta
phase_field = d
parameter_names = 'p eta '
parameter_values = '2 1e-6'
[]
[strain]
type = ADComputeSmallStrain
[]
[elasticity]
type = SmallDeformationIsotropicElasticity
bulk_modulus = K
shear_modulus = G
phase_field = d
degradation_function = g
decomposition = NONE
output_properties = 'elastic_strain psie_active'
outputs = exodus
[]
[stress]
type = ComputeSmallDeformationStress
elasticity_model = elasticity
output_properties = 'stress'
outputs = exodus
[]
[]
[Postprocessors]
[Fy]
type = NodalSum
variable = fy
boundary = top
[]
[]
[Executioner]
type = Transient
solve_type = NEWTON
petsc_options_iname = '-pc_type -pc_factor_mat_solver_package'
petsc_options_value = 'lu superlu_dist '
automatic_scaling = true
nl_rel_tol = 1e-8
nl_abs_tol = 1e-10
dt = 2e-5
end_time = 3.5e-3
fixed_point_max_its = 20
accept_on_max_fixed_point_iteration = true
fixed_point_rel_tol = 1e-8
fixed_point_abs_tol = 1e-10
[]
[Outputs]
exodus = true
print_linear_residuals = false
[]