Combined Nonlinear Hardening Plasticity

Combined isotropic and kinematic plasticity model with nonlinear hardening rules, including a Voce model for isotropic hardening and an Armstrong-Fredrick model for kinematic hardening.

Description

In this numerical approach, a trial stress is calculated at the start of each simulation time increment; the trial stress calculation assumed all of the new strain increment is elastic strain:

The algorithms checks to see if the trial stress state is outside of the yield surface, as shown in the figure to the right. If the stress state is outside of the yield surface, the algorithm recomputes the scalar effective inelastic strain required to return the stress state to the yield surface. This approach is given the name Radial Return because the yield surface used is the von Mises yield surface: in the deviatoric stress space, this yield surface has the shape of a circle, and the scalar inelastic strain is assumed to always be directed at the circle center.

Recompute Iterations on the Effective Plastic Strain Increment

The recompute radial return materials each individually calculate, using the Newton Method, the amount of effective inelastic strain required to return the stress state to the yield surface.

where the change in the iterative effective inelastic strain is defined as the yield surface over the derivative of the yield surface with respect to the inelastic strain increment.

In this model, the linear isotropic hardening function is given by , and kinematic hardening is governed by a backstress evolution equation of the form: , where X is the backstress, and the two coefficients, C and D, represent the evolution of kinematic hardening.

The non-linear equations for Isotropic and Kinematic Hardening are based on Besson et al. (2009) pg. 82–84. The reference uses the nonlinear kinematic hardening rule proposed by Armstrong and Frederick Armstrong et al. (1966), while the isotropic hardening rule follows the Voce isotropic hardening model Voce (1948).

The effective plastic strain increment for combined hardening has the form: where is the isotropic shear modulus, and is the scalar part of (von Mises trial stress - backstress).

The non-linear equations for Isotropic and Kinematic Hardening are based on Besson et al. (2009) pg. 82–84.

This class calculates an effective trial stress, an effective scalar plastic strain increment, and the derivative of the scalar effective plastic strain increment; these values are passed to the RadialReturnBackstressStressUpdateBase to compute the radial return stress increment. This class also computes the plastic strain as a stateful material property.

This class is based on the implicit integration algorithm in Dunne and Petrinic (2005) pg. 146–149.

The ADCombinedNonlinearHardeningPlasticity version of this class uses forward mode automatic differentiation to provide all necessary material property derivatives to assemble a perfect Jacobian (this replaces the approximated tangent operator).

This model can be reduced to a purely linear isotropic model, if the kinematic hardening modulus is set to zero, as the backstress in the effective trial stress will remain zero and will not be updated. Conversely, if only the kinematic hardening modulus is set to a nonzero value, the hardening model will behave purely as linear kinematic.

To model the nonlinear hardening behavior of a material, the constants Q (saturation hardening) and b (rate of hardening) should be set to nonzero values for nonlinear isotropic hardening. Additionally, to capture nonlinear kinematic hardening behavior, the kinematic saturation gamma should be nonzero. For a combined nonlinear hardening model, all constants (Q, b, and gamma) should be set to nonzero values.

The following cyclic stress-strain plots below verify some of the responses

This combined hardening model is verified by plotting cyclic stress-strain curves using the same values of constants from Besson et al. (2009) pg. 87–90. The model's results are compared to those from that reference, confirming that the implementation is functioning as expected. Some of the examples of cyclic hardening plots are shown below:

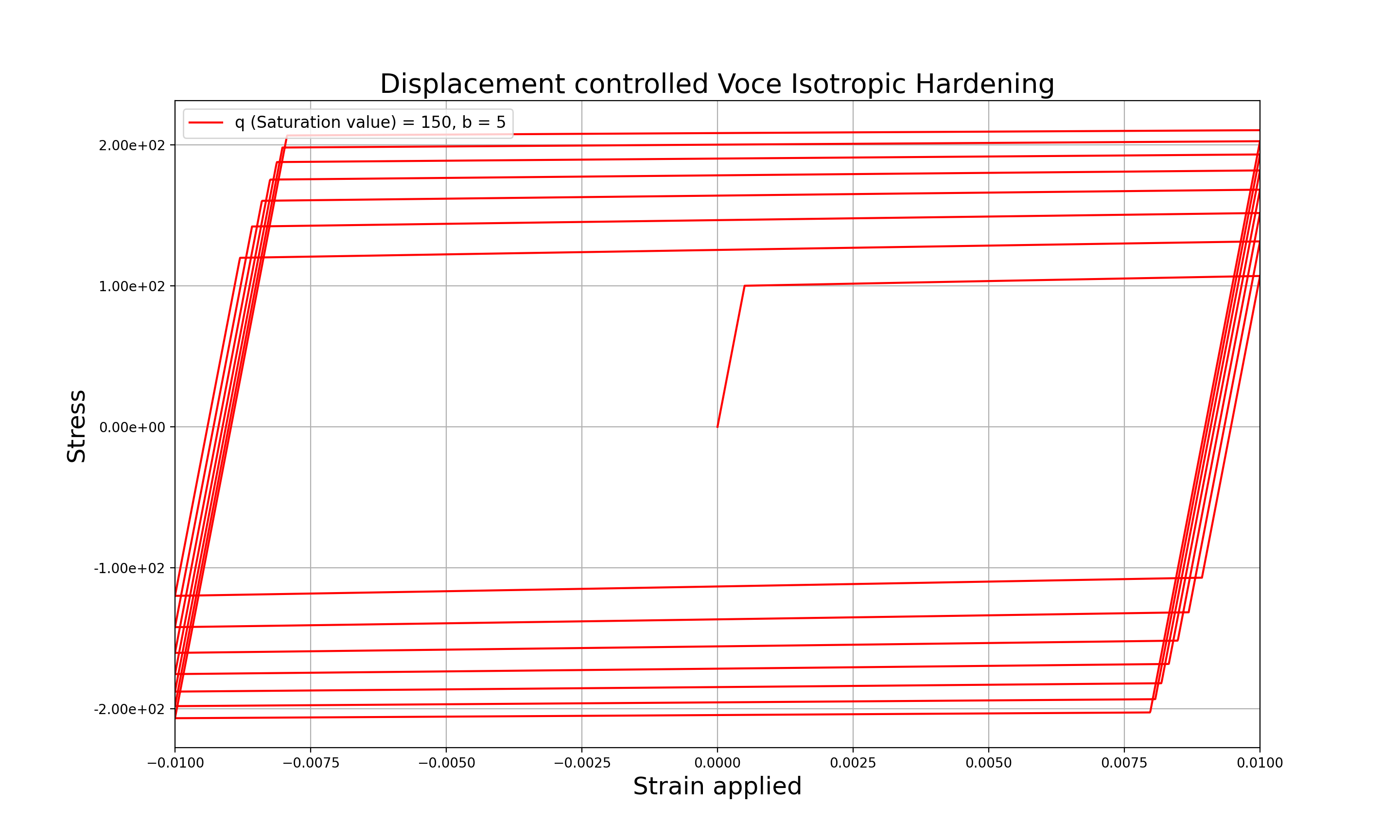
Figure 1: Isotropic Hardening under prescribed symmetric strain

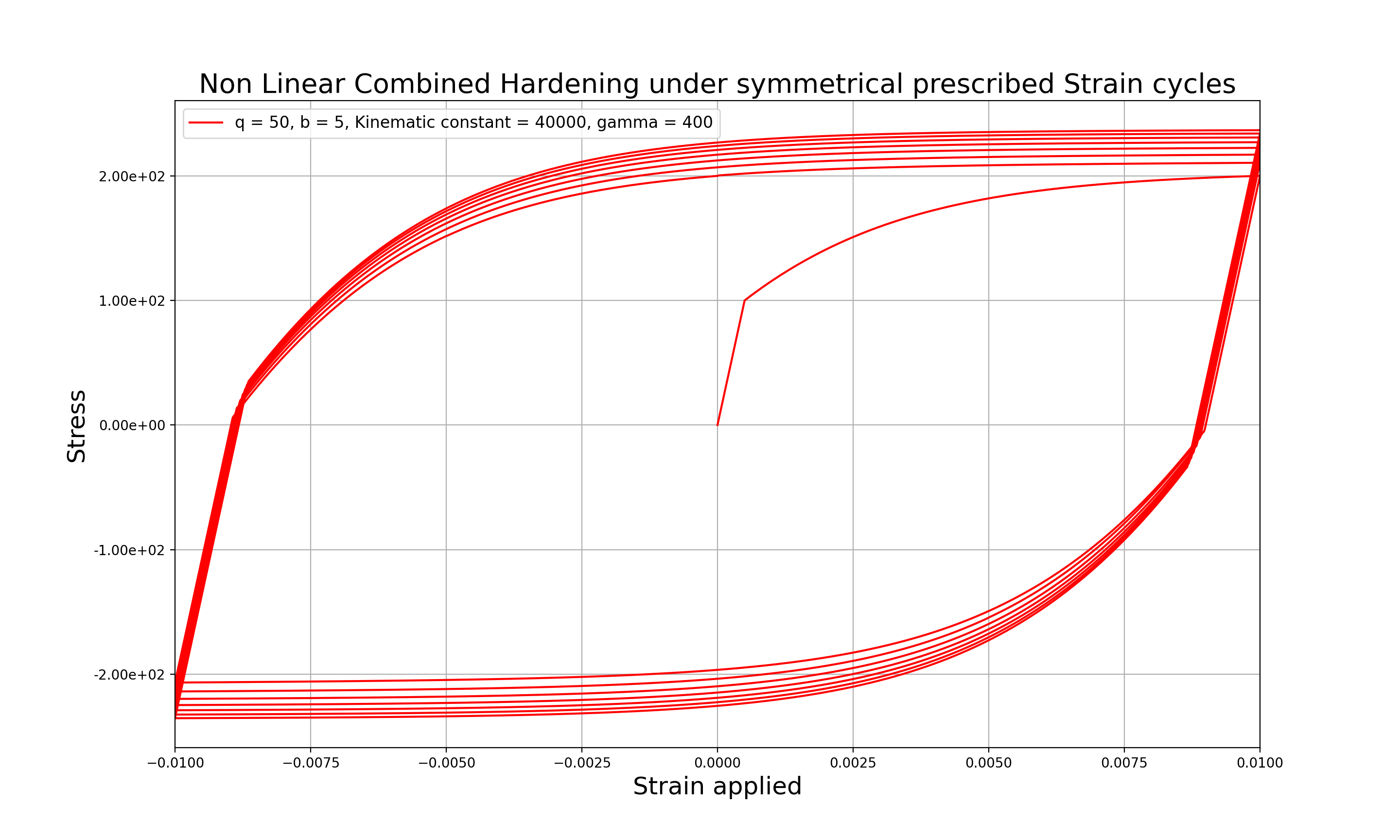
Figure 2: Isotropic and Kinematic Nonlinear Hardening under prescribed symmetric strain

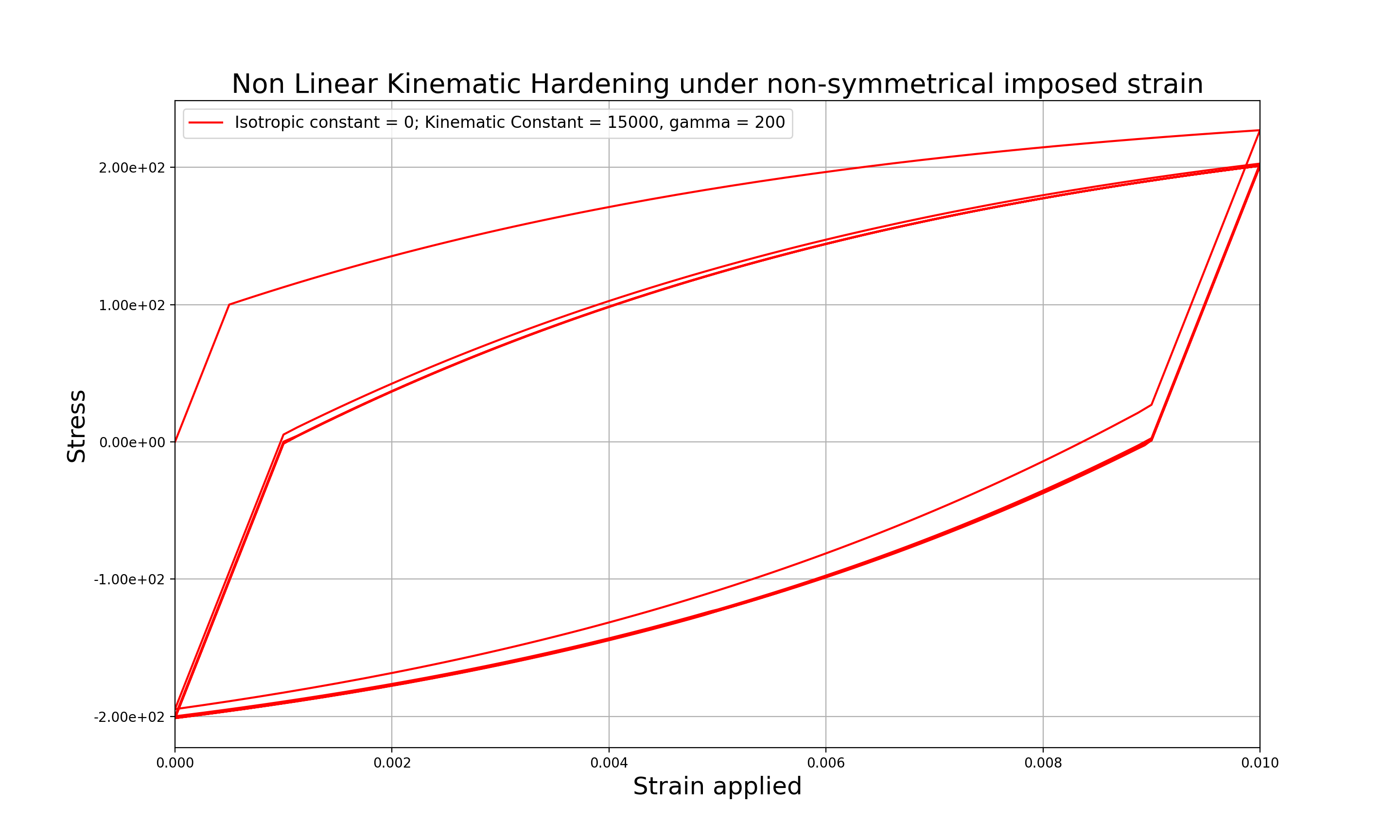
Figure 3: Nonlinear Kinematic Hardening under nonsymmetric imposed strain

Figure 4: 1D Ratcheting under nonsymmetrical imposed stress path due to nonlinear kinematic hardening

Example Input File Syntax

[Materials]
  [combined_plasticity]
    type = CombinedNonlinearHardeningPlasticity
    yield_stress = 100
    isotropic_hardening_constant = 0
    q = 50
    b = 5
    kinematic_hardening_modulus = 40000
    gamma = 400
  []
[]
(moose/modules/solid_mechanics/test/tests/rate_independent_cyclic_hardening/nonlin_isokinharden_symmetric_strain_controlled.i)

CombinedNonlinearHardeningPlasticity must be used in conjunction with this inelastic strain return mapping stress calculator as shown below:

[Materials]
  [radial_return_stress]
    type = ComputeMultipleInelasticStress
    tangent_operator = elastic
    inelastic_models = 'combined_plasticity'
  []
[]
(moose/modules/solid_mechanics/test/tests/rate_independent_cyclic_hardening/nonlin_isokinharden_symmetric_strain_controlled.i)

Input Parameters

  • absolute_tolerance1e-11Absolute convergence tolerance for Newton iteration

    Default:1e-11

    C++ Type:double

    Unit:(no unit assumed)

    Controllable:No

    Description:Absolute convergence tolerance for Newton iteration

  • acceptable_multiplier10Factor applied to relative and absolute tolerance for acceptable convergence if iterations are no longer making progress

    Default:10

    C++ Type:double

    Unit:(no unit assumed)

    Controllable:No

    Description:Factor applied to relative and absolute tolerance for acceptable convergence if iterations are no longer making progress

  • adaptive_substeppingFalseUse adaptive substepping, where the number of substeps is successively doubled until the return mapping model successfully converges or the maximum number of substeps is reached.

    Default:False

    C++ Type:bool

    Unit:(no unit assumed)

    Controllable:No

    Description:Use adaptive substepping, where the number of substeps is successively doubled until the return mapping model successfully converges or the maximum number of substeps is reached.

  • automatic_differentiation_return_mappingFalseWhether to use automatic differentiation to compute the derivative.

    Default:False

    C++ Type:bool

    Unit:(no unit assumed)

    Controllable:No

    Description:Whether to use automatic differentiation to compute the derivative.

  • b0Rate constant for isotropic hardening (b in Voce model)

    Default:0

    C++ Type:double

    Unit:(no unit assumed)

    Controllable:No

    Description:Rate constant for isotropic hardening (b in Voce model)

  • base_nameOptional parameter that defines a prefix for all material properties related to this stress update model. This allows for multiple models of the same type to be used without naming conflicts.

    C++ Type:std::string

    Unit:(no unit assumed)

    Controllable:No

    Description:Optional parameter that defines a prefix for all material properties related to this stress update model. This allows for multiple models of the same type to be used without naming conflicts.

  • blockThe list of blocks (ids or names) that this object will be applied

    C++ Type:std::vector<SubdomainName>

    Unit:(no unit assumed)

    Controllable:No

    Description:The list of blocks (ids or names) that this object will be applied

  • boundaryThe list of boundaries (ids or names) from the mesh where this object applies

    C++ Type:std::vector<BoundaryName>

    Unit:(no unit assumed)

    Controllable:No

    Description:The list of boundaries (ids or names) from the mesh where this object applies

  • constant_onNONEWhen ELEMENT, MOOSE will only call computeQpProperties() for the 0th quadrature point, and then copy that value to the other qps.When SUBDOMAIN, MOOSE will only call computeQpProperties() for the 0th quadrature point, and then copy that value to the other qps. Evaluations on element qps will be skipped

    Default:NONE

    C++ Type:MooseEnum

    Unit:(no unit assumed)

    Options:NONE, ELEMENT, SUBDOMAIN

    Controllable:No

    Description:When ELEMENT, MOOSE will only call computeQpProperties() for the 0th quadrature point, and then copy that value to the other qps.When SUBDOMAIN, MOOSE will only call computeQpProperties() for the 0th quadrature point, and then copy that value to the other qps. Evaluations on element qps will be skipped

  • declare_suffixAn optional suffix parameter that can be appended to any declared properties. The suffix will be prepended with a '_' character.

    C++ Type:MaterialPropertyName

    Unit:(no unit assumed)

    Controllable:No

    Description:An optional suffix parameter that can be appended to any declared properties. The suffix will be prepended with a '_' character.

  • gamma0The nonlinear hardening parameter (gamma) for back stress evolution

    Default:0

    C++ Type:double

    Unit:(no unit assumed)

    Controllable:No

    Description:The nonlinear hardening parameter (gamma) for back stress evolution

  • isotropic_hardening_constantIsotropic hardening slope

    C++ Type:double

    Unit:(no unit assumed)

    Controllable:No

    Description:Isotropic hardening slope

  • isotropic_hardening_functionTrue stress as a function of plastic strain

    C++ Type:FunctionName

    Unit:(no unit assumed)

    Controllable:No

    Description:True stress as a function of plastic strain

  • kinematic_hardening_modulus0Kinematic hardening modulus

    Default:0

    C++ Type:double

    Unit:(no unit assumed)

    Controllable:No

    Description:Kinematic hardening modulus

  • max_inelastic_increment0.0001The maximum inelastic strain increment allowed in a time step

    Default:0.0001

    C++ Type:double

    Unit:(no unit assumed)

    Controllable:No

    Description:The maximum inelastic strain increment allowed in a time step

  • maximum_number_substeps25The maximum number of substeps allowed before cutting the time step.

    Default:25

    C++ Type:unsigned int

    Unit:(no unit assumed)

    Controllable:No

    Description:The maximum number of substeps allowed before cutting the time step.

  • prop_getter_suffixAn optional suffix parameter that can be appended to any attempt to retrieve/get material properties. The suffix will be prepended with a '_' character.

    C++ Type:MaterialPropertyName

    Unit:(no unit assumed)

    Controllable:No

    Description:An optional suffix parameter that can be appended to any attempt to retrieve/get material properties. The suffix will be prepended with a '_' character.

  • q0Saturation value for isotropic hardening (Q in Voce model)

    Default:0

    C++ Type:double

    Unit:(no unit assumed)

    Controllable:No

    Description:Saturation value for isotropic hardening (Q in Voce model)

  • relative_tolerance1e-08Relative convergence tolerance for Newton iteration

    Default:1e-08

    C++ Type:double

    Unit:(no unit assumed)

    Controllable:No

    Description:Relative convergence tolerance for Newton iteration

  • temperatureCoupled Temperature

    C++ Type:std::vector<VariableName>

    Unit:(no unit assumed)

    Controllable:No

    Description:Coupled Temperature

  • use_interpolated_stateFalseFor the old and older state use projected material properties interpolated at the quadrature points. To set up projection use the ProjectedStatefulMaterialStorageAction.

    Default:False

    C++ Type:bool

    Unit:(no unit assumed)

    Controllable:No

    Description:For the old and older state use projected material properties interpolated at the quadrature points. To set up projection use the ProjectedStatefulMaterialStorageAction.

  • use_substep_integration_errorFalseIf true, it establishes a substep size that will yield, at most,the creep numerical integration error given by substep_strain_tolerance.

    Default:False

    C++ Type:bool

    Unit:(no unit assumed)

    Controllable:No

    Description:If true, it establishes a substep size that will yield, at most,the creep numerical integration error given by substep_strain_tolerance.

  • use_substeppingNONEWhether and how to use substepping

    Default:NONE

    C++ Type:MooseEnum

    Unit:(no unit assumed)

    Options:NONE, ERROR_BASED, INCREMENT_BASED

    Controllable:No

    Description:Whether and how to use substepping

  • yield_stressThe point at which plastic strain begins accumulating

    C++ Type:double

    Unit:(no unit assumed)

    Controllable:No

    Description:The point at which plastic strain begins accumulating

  • yield_stress_functionYield stress as a function of temperature

    C++ Type:FunctionName

    Unit:(no unit assumed)

    Controllable:No

    Description:Yield stress as a function of temperature

Optional Parameters

  • apply_strainTrueFlag to apply strain. Used for testing.

    Default:True

    C++ Type:bool

    Unit:(no unit assumed)

    Controllable:No

    Description:Flag to apply strain. Used for testing.

  • control_tagsAdds user-defined labels for accessing object parameters via control logic.

    C++ Type:std::vector<std::string>

    Unit:(no unit assumed)

    Controllable:No

    Description:Adds user-defined labels for accessing object parameters via control logic.

  • effective_inelastic_strain_nameeffective_plastic_strainName of the material property that stores the effective inelastic strain

    Default:effective_plastic_strain

    C++ Type:std::string

    Unit:(no unit assumed)

    Controllable:No

    Description:Name of the material property that stores the effective inelastic strain

  • enableTrueSet the enabled status of the MooseObject.

    Default:True

    C++ Type:bool

    Unit:(no unit assumed)

    Controllable:Yes

    Description:Set the enabled status of the MooseObject.

  • implicitTrueDetermines whether this object is calculated using an implicit or explicit form

    Default:True

    C++ Type:bool

    Unit:(no unit assumed)

    Controllable:No

    Description:Determines whether this object is calculated using an implicit or explicit form

  • seed0The seed for the master random number generator

    Default:0

    C++ Type:unsigned int

    Unit:(no unit assumed)

    Controllable:No

    Description:The seed for the master random number generator

  • substep_strain_tolerance0.1Maximum ratio of the initial elastic strain increment at start of the return mapping solve to the maximum inelastic strain allowable in a single substep. Reduce this value to increase the number of substeps

    Default:0.1

    C++ Type:double

    Unit:(no unit assumed)

    Controllable:No

    Description:Maximum ratio of the initial elastic strain increment at start of the return mapping solve to the maximum inelastic strain allowable in a single substep. Reduce this value to increase the number of substeps

  • use_displaced_meshFalseWhether or not this object should use the displaced mesh for computation. Note that in the case this is true but no displacements are provided in the Mesh block the undisplaced mesh will still be used.

    Default:False

    C++ Type:bool

    Unit:(no unit assumed)

    Controllable:No

    Description:Whether or not this object should use the displaced mesh for computation. Note that in the case this is true but no displacements are provided in the Mesh block the undisplaced mesh will still be used.

Advanced Parameters

  • internal_solve_full_iteration_historyFalseSet true to output full internal Newton iteration history at times determined by `internal_solve_output_on`. If false, only a summary is output.

    Default:False

    C++ Type:bool

    Unit:(no unit assumed)

    Controllable:No

    Description:Set true to output full internal Newton iteration history at times determined by `internal_solve_output_on`. If false, only a summary is output.

  • internal_solve_output_onon_errorWhen to output internal Newton solve information

    Default:on_error

    C++ Type:MooseEnum

    Unit:(no unit assumed)

    Options:never, on_error, always

    Controllable:No

    Description:When to output internal Newton solve information

Debug Parameters

  • output_propertiesList of material properties, from this material, to output (outputs must also be defined to an output type)

    C++ Type:std::vector<std::string>

    Unit:(no unit assumed)

    Controllable:No

    Description:List of material properties, from this material, to output (outputs must also be defined to an output type)

  • outputsnone Vector of output names where you would like to restrict the output of variables(s) associated with this object

    Default:none

    C++ Type:std::vector<OutputName>

    Unit:(no unit assumed)

    Controllable:No

    Description:Vector of output names where you would like to restrict the output of variables(s) associated with this object

Outputs Parameters

References

  1. Peter J Armstrong, Charles O Frederick, and others. A mathematical representation of the multiaxial Bauschinger effect. Volume 731. Berkeley Nuclear Laboratories Berkeley, CA, 1966.[BibTeX]
  2. Jacques Besson, Georges Cailletaud, Jean-Louis Chaboche, and Samuel Forest. Non-linear mechanics of materials. Volume 167. Springer Science & Business Media, 2009.[BibTeX]
  3. Fionn Dunne and Nik Petrinic. Introduction to Computational Plasticity. Oxford University Press on Demand, 2005.[BibTeX]
  4. Eric Voce. The relationship between stress and strain for homogeneous deformation. Journal of the Institute of Metals, 74:537–562, 1948.[BibTeX]