Step 4: Make the Mobility a Function
The input file for this step can be found here: s4_mobility.i
Input File Changes
We are going to make two changes to our simulation. First, we will make the mobility a function instead of a constant. Then, we will check if the surface is decomposing to 39.5% chromium phase as the material balance says it should. Both of these changes are primarily in the materials block. We will use a DerivativeParsedMaterial to define the equation for mobility, similar to how we defined the free energy density. We will have to remove it from the constants block. Then we will add another material to check if each element is in the chromium phase. The materials block now looks like this:
[Materials]
# d is a scaling factor that makes it easier for the solution to converge
# without changing the results. It is defined in each of the first three
# materials and must have the same value in each one.
[kappa] # Gradient energy coefficient (eV nm^2/mol)
type = GenericFunctionMaterial
prop_names = 'kappa_c'
prop_values = '8.125e-16*6.24150934e+18*1e+09^2*1e-27'
# kappa_c*eV_J*nm_m^2*d
[]
[mobility] # Mobility (nm^2 mol/eV/s)
type = DerivativeParsedMaterial
f_name = M
args = c
constant_names = 'Acr Bcr Ccr Dcr
Ecr Fcr Gcr
Afe Bfe Cfe Dfe
Efe Ffe Gfe
nm_m eV_J d'
constant_expressions = '-32.770969 -25.8186669 -3.29612744 17.669757
37.6197853 20.6941796 10.8095813
-31.687117 -26.0291774 0.2286581 24.3633544
44.3334237 8.72990497 20.956768
1e+09 6.24150934e+18 1e-27'
function = 'nm_m^2/eV_J/d*((1-c)^2*c*10^
(Acr*c+Bcr*(1-c)+Ccr*c*log(c)+Dcr*(1-c)*log(1-c)+
Ecr*c*(1-c)+Fcr*c*(1-c)*(2*c-1)+Gcr*c*(1-c)*(2*c-1)^2)
+c^2*(1-c)*10^
(Afe*c+Bfe*(1-c)+Cfe*c*log(c)+Dfe*(1-c)*log(1-c)+
Efe*c*(1-c)+Ffe*c*(1-c)*(2*c-1)+Gfe*c*(1-c)*(2*c-1)^2))'
derivative_order = 1
outputs = exodus
[]
[local_energy] # Local free energy function (eV/mol)
type = DerivativeParsedMaterial
f_name = f_loc
args = c
constant_names = 'A B C D E F G eV_J d'
constant_expressions = '-2.446831e+04 -2.827533e+04 4.167994e+03 7.052907e+03
1.208993e+04 2.568625e+03 -2.354293e+03
6.24150934e+18 1e-27'
function = 'eV_J*d*(A*c+B*(1-c)+C*c*log(c)+D*(1-c)*log(1-c)+
E*c*(1-c)+F*c*(1-c)*(2*c-1)+G*c*(1-c)*(2*c-1)^2)'
derivative_order = 2
[]
[precipitate_indicator] # Returns 1/625 if precipitate
type = ParsedMaterial
f_name = prec_indic
args = c
function = if(c>0.6,0.0016,0)
[]
[]
Note that the area of our surface is 625 , and . Within the different materials, the argument "block = 0" is not included. It can save time if we can define common arguments once rather than in each material. To do this, we include a global parameters block.
[GlobalParams]
block = 0 # The generated mesh is used for all materials and kernels
[]
The mobility equation is now ready to run. However, the chromium phase fraction will not be output. In order to output it we add a Postprocessor.
[precipitate_area] # Fraction of surface devoted to precipitates
type = ElementIntegralMaterialProperty
mat_prop = prec_indic
[]
This brings the number of Postprocessors up to 6.
Results
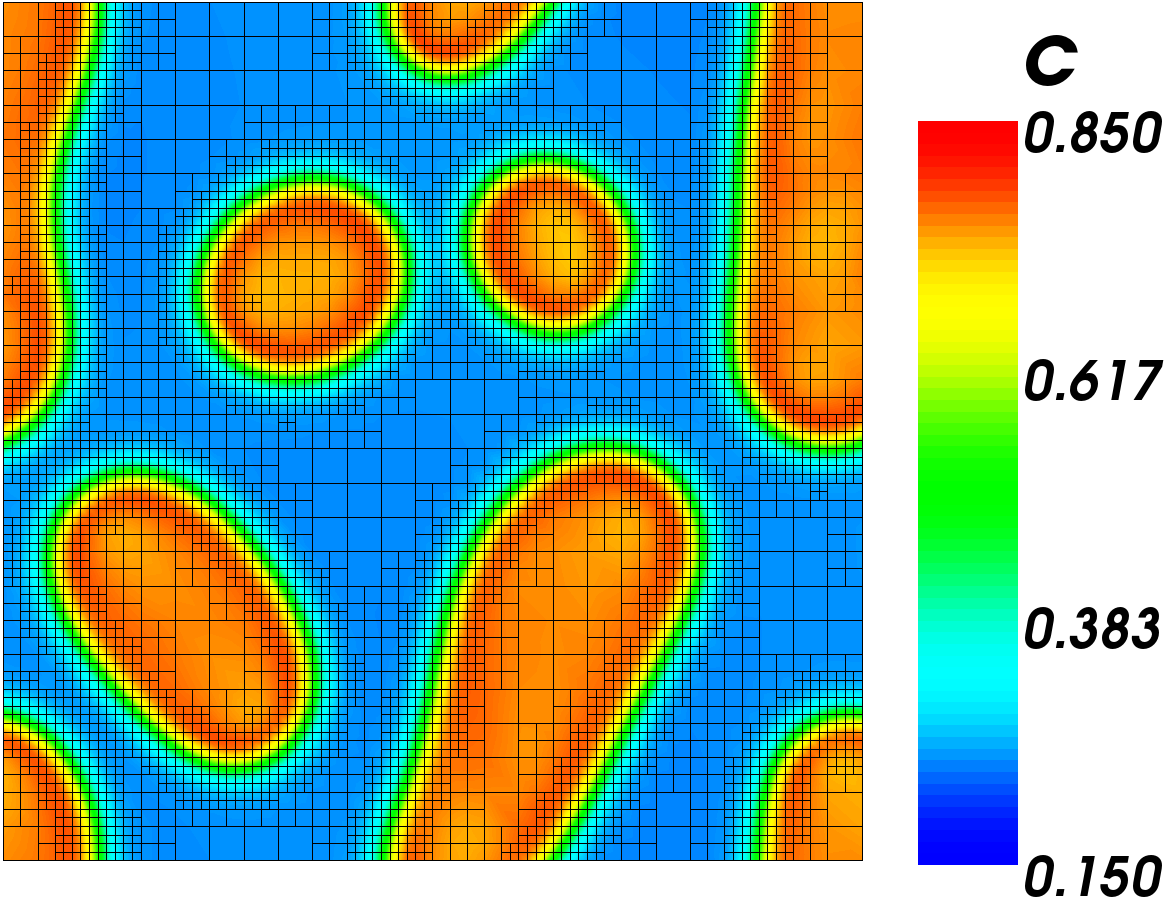
simulation result
The first figure to the right shows the results of this simulation. As you can see, changing the mobility to a function reduced the number of features. The second figure shows the fraction of the surface covered with the chromium phase as a function of time. It is very close to the 39.5% we calculated, which is promising. It is not exact because of the concentration gradients at the phase interfaces.
If you still have the residual magnitudes outputting to the screen, you may have noticed that the magnitudes changed this time. The residual for the concentration is now several orders of magnitude smaller than the residual for chemical potential. In our next simulation we will scale the concentration variable so that this is not the case.
Continue
We are almost done. Next, we will calculate the total free energy of the surface and look for its S-curve.
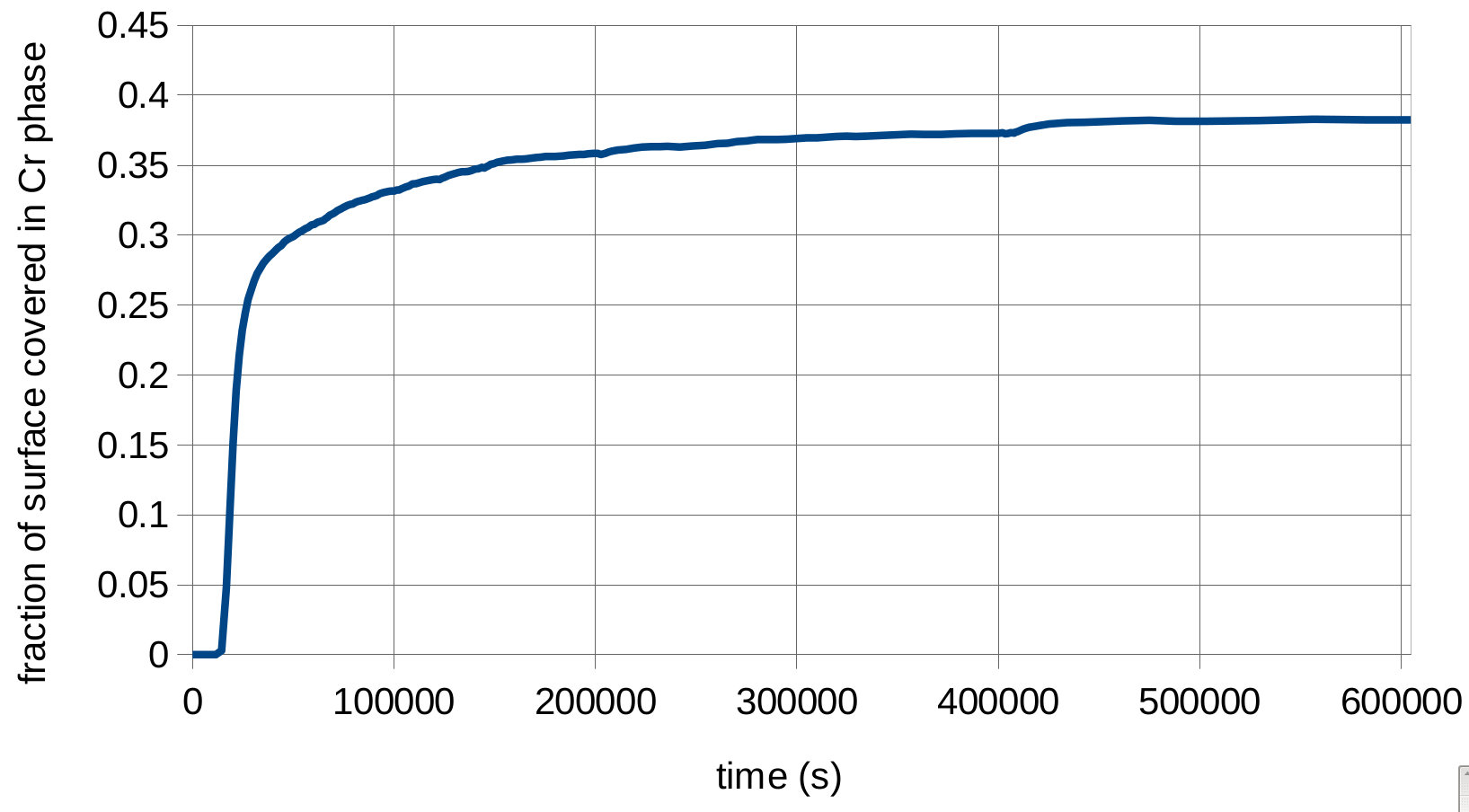
chromium phase fraction