Theory for the New Lagrangian Kernels

Introduction

The new kernel system provides two options for enforcing stress equilibrium over a domain described by a map between the reference configuration of the body, defined as with coordinates , and the current configuration of the body defined as with coordinates . The mathematics here uses upper case letters to define quantities related to the reference configuration and lower case letters to define quantities related to the current configuration. Specifically, denotes a spatial gradient with respect to the current coordinates while denotes a gradient with respect to the reference coordinates. Figure 1 describes these two frames of reference. The new kernel system current supports three coordinate systems: 3D Cartesian coordinates, 2D axisymmetric cylindrical coordinates, and 1D centrosymmetric spherical coordinates.

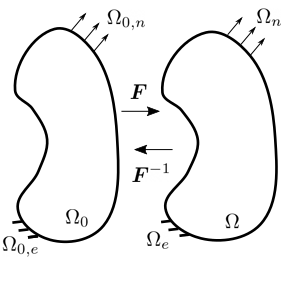
Figure 1: Summary of the reference and current configurations with key quantities.

The total Lagrangian theory enforces the equilibrium condition mapped back to the reference configuration, weakly solving the differential equation: where is the 1st Piola-Kirchhoff stress, are the body forces in the updated configuration, are the boundary normals in the reference configuration, are the tractions in the updated configuration, is the displacement field, and are imposed displacement boundary conditions.

The updated Lagrangian theory enforces the equilibrium condition on the current configuration: where is the Cauchy stress.

It is more natural and common to define the constitutive response for the total Lagrangian formulation as the 1st Piola Kirchhoff stress as a function of the deformation gradient, updated Lagrangian formulation as the Cauchy stress as a function of the deformation gradient, , with the deformation gradient defined as with the Kronecker Delta. However, the Cauchy stress and the 1st Piola Kirchhoff stress are related and so it is possible to convert a "native" Cauchy stress constitutive model to the 1st Piola-Kirchhoff stress and vice versa.

If the boundary conditions, body force, and constitutive model are all identical then the updated and total Lagrangian formulations will return exactly the same results. There is no difference in the final results when using a updated Lagrangian or total Lagrangian model.

However, at times one formulation may be more convenient than another. For example, the homogenization system system only works with the total Lagrangian kernel because of the difficulty in including the extra homogenization field in the kinematic spatial derivatives. In theory it can be more efficient to couple a "native" Cauchy stress constitutive model to the updated Lagrangian configuration and a "native" 1st Piola-Kirchhoff model to the total Lagrangian configuration. However, the currently-implemented material system always coverts Cauchy stress to 1st Piola-Kirchhoff stress and vice-versa so that models can be used with either the updated or total Lagrangian kernels.

Both of these models degenerate to the same formulation for small kinematic theory: where is the small (engineering) stress and there is now no difference between the current and reference configurations. Both the updated and total kernels both both large and small deformation theories. The user can switch between them by setting the large_kinematics flag to true for large deformation theory and false for small deformation theory. This flag applies to the kernels, the strain calculator, the homogenization system, and for many models, the constitutive models for calculating the stress. As such, it is often convenient to set it in the GlobalParams section of the input file so that you can easily switch between the two.

The use_displaced_mesh Flag

In MOOSE the use_displaced_mesh flag indicates whether gradients and integrals are with respect to the current (true) or reference (false) configurations. With the new Lagrangian the only object that needs to have use_displaced_mesh set is the updated Lagrangian when large_kinematics = true. The kernel enforces this condition with an error. For all other objects in the new mechanics system the flag should be set to false.

The SolidMechanics/QuasiStatic can be used to easily coordinate the values of this flag and the use_displaced_mesh flag.

Coupling to the Lagrangian kernels

Modules expecting to couple to the stress material property, which represented the Cauchy stress in the old material system, should now couple to cauchy_stress or pk1_stress instead.