AD Viscoplasticity Stress Update

Description

ADViscoplasticityStressUpdate implements the Gurson-Tvergaard-Needleman (GTN) and Leblond-Perrin-Suqeut (LPS) following the theory described above. ADViscoplasticityStressUpdate uses similar techniques as ADRadialReturnStressUpdate to compute the gauge stress in order to correctly calculate the plastic strain in a porous material. ADViscoplasticityStressUpdate must be used in conjunction with ADComputeMultiplePorousInelasticStress in order to capture the porosity evolution.

Theory

As pores nucleate within a material system, the dissipative potential that governs overall stress-strain response and drives local void growth mechanisms is enhanced. Simply put, the constitutive behavior of a material and the evolution of porosity within are highly coupled processes. In high-temperature and other extreme environments, this potential should include effects of viscoplasticity and diffusion.

Homogenization of a composite material's plastic potential can be accomplished using the Bishop and Hill (1951) upper-bound theorem for dissipation, which says that any possible dissipation field solved at the macroscopic level is an upper bound to the volume average of local dissipation within a material system.

In many continuum level modeling problems, the simulation length scale is larger than individual voids themselves, and therefore methods in homogenization are required to model the voided material response with an approximated, simplified medium. These methods aim to match the dissipative potential of the true medium Figure 1, thereby ensuring accurate stress-strain constitutive behavior of the porous material system.

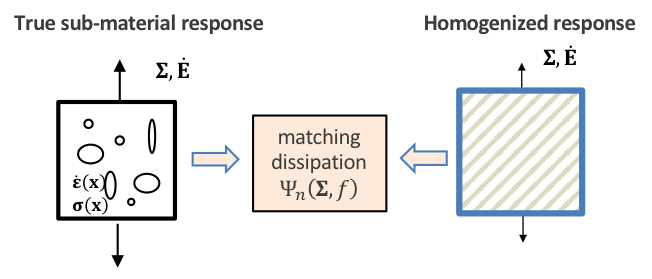
Figure 1: Schematic comparing the true sub-material response and the homogenized response and showing that the two methods match energy dissipation.

Gurson (1977) employed this approach to solve for dissipation in a purely-plastic (rate-insensitive) material, and derived an exact expression for the velocity and strain fields within a unit cell based on isotropic expressions of the Rice and Tracey (1969) fields. The solution to these velocity fields was derived using boundary conditions of strain at the surface of the unit cell, local incompressibility of the material system, and an overall minimization of work to bring the approximate upper-bound solution as close as possible to the true solution. In Gurson's formulation, it should be noted that despite incompressibility of the material itself, the overall unit cell (void + material) is in fact compressible due to the void. Therefore, void growth, can be modeled simply based on overall dilatation:

The exact result for average dissipation in the unit cell was correlated against an analytical solution so that it would be useful for application in finite element codes for large-scale component analysis. Several fitting parameters were introduced into Gurson's model by Tvergaard and Needleman (1984) to account for a periodic array of voids (rather than the original unit cell), leading to the famous GTN model that is the most widely-used damage and porosity evolution model for ductile materials.

Leblond et al. (1994) (LPS) extended the GTN model to account for rate-sensitive plastics. While far less common than the rate-insensitive GTN model, the work by Leblond et al. generated a similar analytical solution to GTN, but accounted for dissipation in the material, making it also very accessible to finite element implementation. It is expected that differences between rate-sensitive (i.e. LPS) and rate-insensitive (i.e. GTN) plasticity will become significant at lower temperatures and stresses. As such, the LPS model is selected for describing dissipation in a rate-sensitive voided material. In the case of a single dissipative potential, described by a Norton-type power law:

(1) (2) Here, the gauge stress, , is used to translate applied stress and porosity to strain rate response in a power law creeping material with rate-sensitivity factor , is given via the minimization of the residual : where is a rate sensitivity factor. The law proposed by Leblond et al. (1994)reduces exactly to the Gurson (1977) model when using a rate-insensitive exponent.

Implementation

The inelastic strain is currently calculated explicitly, where the strain rate is calculated via, (3) By taking the derivative of Eq. (3) with respect to the gauge stress, the familiar Norton power law is formed, (4) providing a clear link between traditional power law creep solves; by replacing utilized in traditional power law creep equations with a gauge stress, the exact strain dissipation is captured due to the act of homogenization.

Using the LPS model, the gauge stress is calculated by minimizing the residual, (5)

The rate sensitivity factor is a function of the strain rate stress exponent, gauge stress, and equivalent stress, (6) where is a shape factor that depends on the pore shape: (7)

In addition, the mean stress utilized in Eq. (6) is different depending on the shape of the pore, (8)

The GTN can be solved in exactly the same manner as the LPS model by taking in Eq. (5) and Eq. (7), reducing to,

Once a solution for is found, the strain rate can be determined using Eq. (3) with the relationship,

Example Input Files

In all cases, ADViscoplasticityStressUpdate must be combined with ADComputeMultiplePorousInelasticStress in order to calculate the stress and capture the porosity evolution of the material:

[Materials]
  [./elasticity_tensor]
    type = ADComputeIsotropicElasticityTensor
    youngs_modulus = 1e10
    poissons_ratio = 0.3
  [../]
  [./stress]
    type = ADComputeMultipleInelasticStress
    inelastic_models = lps
    outputs = all
  [../]
  [./porosity]
    type = ADPorosityFromStrain
    initial_porosity = 0.1
    inelastic_strain = 'combined_inelastic_strain'
    outputs = 'all'
  [../]

  [./lps]
    type = ADViscoplasticityStressUpdate
    coefficient = 'coef'
    power = 3
    outputs = all
    relative_tolerance = 1e-11
  [../]
  [./coef]
    type = ADParsedMaterial
    property_name = coef
    # Example of creep power law
    expression = '1e-18 * exp(-4e4 / 1.987 / 1200)'
  [../]
[]

In this case, the power law coefficient defined in Eq. (4) is provided as an example here as a ParsedMaterial. Note, if necessary, the coefficient must be provided as an AD material if variables or variable dependent materials are utilized to calculate coefficient.

If several different stress exponents are required, separate ADViscoplasticityStressUpdate must be specified, and combined in ADComputeMultiplePorousInelasticStress:

Here, materials calculated by ADViscoplasticityStressUpdate are prepended with base_name to separate their contributions to the overall system. Note, this is different than the base_name provided in the Solid Mechanics Physics

[Materials]
  [./elasticity_tensor]
    type = ADComputeIsotropicElasticityTensor
    youngs_modulus = 1e10
    poissons_ratio = 0.3
  [../]
  [./stress]
    type = ADComputeMultipleInelasticStress
    inelastic_models = 'one two'
    outputs = all
  [../]
  [./porosity]
    type = ADPorosityFromStrain
    initial_porosity = 0.1
    inelastic_strain = 'combined_inelastic_strain'
    outputs = 'all'
  [../]

  [./one]
    type = ADViscoplasticityStressUpdate
    coefficient = 'coef_3'
    power = 3
    base_name = 'lps_1'
    outputs = all
    relative_tolerance = 1e-11
  [../]
  [./two]
    type = ADViscoplasticityStressUpdate
    coefficient = 1e-10
    power = 1
    base_name = 'lps_3'
    outputs = all
    relative_tolerance = 1e-11
  [../]
  [./coef]
    type = ADParsedMaterial
    property_name = coef_3
    # Example of creep power law
    coupled_variables = temp
    expression = '0.5e-18 * exp(-4e4 / 1.987 / temp)'
  [../]
[]

Input Parameters

References