Dynamics
Dynamic problems like the response of a multi degree of freedom structure to external forcing and wave propagation in a medium can also be solved using the Solid Mechanics module.
The equation of motion for a typical dynamics problem has the following format:
Here, is the mass matrix, is the damping matrix, is the stiffness matrix and is the vector of external forces acting at the nodes. , and are the vector of displacement, velocity and acceleration at the nodes, respectively.
Time integration
To solve the above equation for , an appropriate time integration scheme needs to be chosen. Newmark (Newmark, 1959) and Hilber-Hughes-Taylor (HHT) (Hughes, 2000) time integration schemes are two of the commonly used methods in dynamics.
Newmark time integration
In Newmark time integration, the acceleration and velocity at are written in terms of the displacement, velocity and acceleration at time and the displacement at using the NewmarkAccelAux and NewmarkVelAux Aux Kernels, respectively.
In the above equations, and are Newmark time integration parameters. Substituting the above two equations into the equation of motion will result in a linear system of equations () from which can be estimated.
For and , the Newmark time integration method is implicit and unconditionally stable. This is the constant average acceleration method with no numerical damping. This is recommended only when a constant timestep is used throughout the simulation. If for some reason, the simulation does not converge and the timestep is halved, this time integration method with no numerical damping can result in high frequency noise.
and results in the linear acceleration method where the acceleration is linearly varying between and .
and is identical to the central difference method.
For in structural dynamics problems, the Newmark method is unconditionally stable irrespective of the time-step . For , the Newmark method is at least second order accurate; it is first order accurate for all other values of .
Hilber-Hughes-Taylor time integration
The HHT time integration scheme is built upon Newmark time integration method. Here, in addition to the Newmark equations, the equation of motion is also altered resulting in:
Here, is the HHT parameter. For , and , the HHT method is at least second-order accurate and unconditionally stable. For non-zero values of , the response at high frequencies (above ) are numerically damped, provided and are defined as above.
More details about the Newmark method and HHT method can be found in these lecture notes.
Rayleigh damping
This is the most common form of structural damping used in dynamic problems. Here, the damping matrix () is assumed to be a linear combination of the mass and stiffness matrices, i.e., . Here, and are the mass and stiffness dependent Rayleigh damping parameters, respectively.
The equation of motion in the presence of Rayleigh damping is:
The degree of damping in the system depends on the coefficients and as follows: (1)
where, is the damping ratio of the system as a function of frequency . For example, the damping ratio as a function of frequency for and is presented in Figure 1. Note that has units of rad/s and used in the figure has units of Hz.
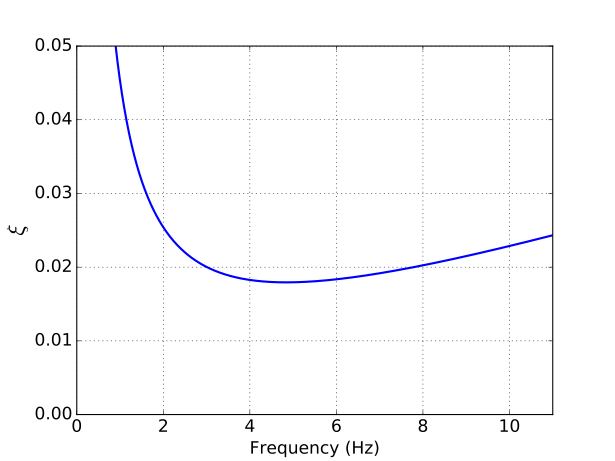
Figure 1: Damping ratio as a function of frequency.
To model a constant damping ratio using Rayleigh damping, the aim is to find and such that the is close to the target damping ratio , which is a constant value, between the frequency range . This can be achieved by minimizing the difference between and for all the frequencies between and , i.e., if
Then, and results in two equations that are linear in and . Solving these two linear equations simultaneously gives:
A similar method can be used to estimate and for non-constant damping ratios.
Implementation and Usage
In the MOOSE framework, the mass and stiffness matrices are not explicitly calculated. Only the residuals are calculated. To get the residual, the equation of motion (with Rayleigh damping and HHT time integration) can be written as:
Here, is the density of the material and is the stress tensor. The weak form of the above equation is used to get the residuals.
The first two terms to the left that contain are calculated in the InertialForce kernel. , , and need to be passed as input to the InertialForce kernel.
The next two terms to the left involving are calculated in DynamicStressDivergenceTensors.
Note that the time derivative of and are approximated as follows:
The input file syntax for calculating the residual due to both the Inertial force and the DynamicStressDivergenceTensors is:
Here, ./DynamicSolidMechanics is the action that calls the DynamicStressDivergenceTensors kernel.
Finally, when using HHT time integration method, external forces like gravity and pressure also require as input.
For dynamic problems, it is recommended to use PresetDisplacement and PresetAcceleration for prescribing the displacement and acceleration at a boundary, respectively.
DynamicStressDivergenceTensors uses the undisplaced mesh by default but kernels such as InertialForce and Gravity, and boundary conditions such as Pressure use the displaced mesh by default. All calculations should be performed either using the undisplaced mesh (recommended for small strain problems) or the displaced mesh (recommended for finite strain problems). Therefore, use_displaced_mesh parameter should be appropriately set for all the kernels and boundary conditions.
Static Initialization
To initialize the system under a constant initial loading such as gravity, an initial static analysis can be conducted by turning off all the dynamics related Kernels and AuxKernels such as InertialForce, NewmarkVelAux and NewmarkAccelAux for the first time step. To turn off stiffness proportional Rayleigh damping for the first time step static_initialization flag can be set to true in DynamicSolidMechanics or DynamicStressDivergenceTensors. An example of static initialization can be found in this following test:
# One 3D element under ramped displacement loading.
#
# loading in z direction:
# time : 0.0 0.1 0.2 0.3
# disp : 0.0 0.0 -0.01 -0.01
# Gravity is applied in y direction. To equilibrate the system
# under gravity, a static analysis is run in the first time step
# by turning off the inertial terms. (see controls block and
# DynamicSolidMechanics block).
# Result: The displacement at the top node in the z direction should match
# the prescribed displacement. Also, the z acceleration should
# be two triangular pulses, one peaking at 0.1 and another peaking at
# 0.2.
# The y displacement would be offset by the gravity displacement.
# Also the y acceleration and velocity should be zero until the loading in
# the z direction starts (i.e, until 0.1s)
# Note: The time step used in the displacement data file should match
# the simulation time step (dt and dtmin in the Executioner block).
[Mesh<<<{"href": "../../syntax/Mesh/index.html"}>>>]
type = GeneratedMesh
dim = 3 # Dimension of the mesh
nx = 1 # Number of elements in the x direction
ny = 1 # Number of elements in the y direction
nz = 1 # Number of elements in the z direction
xmin = 0.0
xmax = 1
ymin = 0.0
ymax = 1
zmin = 0.0
zmax = 1
allow_renumbering = false # So NodalVariableValue can index by id
[]
[Variables<<<{"href": "../../syntax/Variables/index.html"}>>>] # variables that are solved
[./disp_x]
[../]
[./disp_y]
[../]
[./disp_z]
[../]
[]
[AuxVariables<<<{"href": "../../syntax/AuxVariables/index.html"}>>>] # variables that are calculated for output
[./accel_x]
[../]
[./vel_x]
[../]
[./accel_y]
[../]
[./vel_y]
[../]
[./accel_z]
[../]
[./vel_z]
[../]
[./stress_xx]
order<<<{"description": "Specifies the order of the FE shape function to use for this variable (additional orders not listed are allowed)"}>>> = CONSTANT
family<<<{"description": "Specifies the family of FE shape functions to use for this variable"}>>> = MONOMIAL
[../]
[./strain_xx]
order<<<{"description": "Specifies the order of the FE shape function to use for this variable (additional orders not listed are allowed)"}>>> = CONSTANT
family<<<{"description": "Specifies the family of FE shape functions to use for this variable"}>>> = MONOMIAL
[../]
[./stress_yy]
order<<<{"description": "Specifies the order of the FE shape function to use for this variable (additional orders not listed are allowed)"}>>> = CONSTANT
family<<<{"description": "Specifies the family of FE shape functions to use for this variable"}>>> = MONOMIAL
[../]
[./strain_yy]
order<<<{"description": "Specifies the order of the FE shape function to use for this variable (additional orders not listed are allowed)"}>>> = CONSTANT
family<<<{"description": "Specifies the family of FE shape functions to use for this variable"}>>> = MONOMIAL
[../]
[./stress_zz]
order<<<{"description": "Specifies the order of the FE shape function to use for this variable (additional orders not listed are allowed)"}>>> = CONSTANT
family<<<{"description": "Specifies the family of FE shape functions to use for this variable"}>>> = MONOMIAL
[../]
[./strain_zz]
order<<<{"description": "Specifies the order of the FE shape function to use for this variable (additional orders not listed are allowed)"}>>> = CONSTANT
family<<<{"description": "Specifies the family of FE shape functions to use for this variable"}>>> = MONOMIAL
[../]
[]
[Kernels<<<{"href": "../../syntax/Kernels/index.html"}>>>]
[./DynamicSolidMechanics<<<{"href": "../../syntax/Kernels/DynamicSolidMechanics/index.html"}>>>] # zeta*K*vel + K * disp
displacements<<<{"description": "The nonlinear displacement variables for the problem"}>>> = 'disp_x disp_y disp_z'
stiffness_damping_coefficient<<<{"description": "Name of material property or a constant real number defining stiffness Rayleigh parameter (zeta)."}>>> = 0.000025
static_initialization<<<{"description": "Set to true get the system to equilibrium under gravity by running a quasi-static analysis (by solving Ku = F) in the first time step."}>>> = true #turns off rayliegh damping for the first time step to stabilize system under gravity
[../]
[./inertia_x] # M*accel + eta*M*vel
type = InertialForce<<<{"description": "Calculates the residual for the inertial force ($M \\cdot acceleration$) and the contribution of mass dependent Rayleigh damping and HHT time integration scheme ($\\eta \\cdot M \\cdot ((1+\\alpha)velq2-\\alpha \\cdot vel-old) $)", "href": "../../source/kernels/InertialForce.html"}>>>
variable<<<{"description": "The name of the variable that this residual object operates on"}>>> = disp_x
velocity<<<{"description": "velocity variable"}>>> = vel_x
acceleration<<<{"description": "acceleration variable"}>>> = accel_x
beta<<<{"description": "beta parameter for Newmark Time integration"}>>> = 0.25 # Newmark time integration
gamma<<<{"description": "gamma parameter for Newmark Time integration"}>>> = 0.5 # Newmark time integration
eta<<<{"description": "Name of material property or a constant real number defining the eta parameter for the Rayleigh damping."}>>> = 19.63
[../]
[./inertia_y]
type = InertialForce<<<{"description": "Calculates the residual for the inertial force ($M \\cdot acceleration$) and the contribution of mass dependent Rayleigh damping and HHT time integration scheme ($\\eta \\cdot M \\cdot ((1+\\alpha)velq2-\\alpha \\cdot vel-old) $)", "href": "../../source/kernels/InertialForce.html"}>>>
variable<<<{"description": "The name of the variable that this residual object operates on"}>>> = disp_y
velocity<<<{"description": "velocity variable"}>>> = vel_y
acceleration<<<{"description": "acceleration variable"}>>> = accel_y
beta<<<{"description": "beta parameter for Newmark Time integration"}>>> = 0.25
gamma<<<{"description": "gamma parameter for Newmark Time integration"}>>> = 0.5
eta<<<{"description": "Name of material property or a constant real number defining the eta parameter for the Rayleigh damping."}>>> = 19.63
[../]
[./inertia_z]
type = InertialForce<<<{"description": "Calculates the residual for the inertial force ($M \\cdot acceleration$) and the contribution of mass dependent Rayleigh damping and HHT time integration scheme ($\\eta \\cdot M \\cdot ((1+\\alpha)velq2-\\alpha \\cdot vel-old) $)", "href": "../../source/kernels/InertialForce.html"}>>>
variable<<<{"description": "The name of the variable that this residual object operates on"}>>> = disp_z
velocity<<<{"description": "velocity variable"}>>> = vel_z
acceleration<<<{"description": "acceleration variable"}>>> = accel_z
beta<<<{"description": "beta parameter for Newmark Time integration"}>>> = 0.25
gamma<<<{"description": "gamma parameter for Newmark Time integration"}>>> = 0.5
eta<<<{"description": "Name of material property or a constant real number defining the eta parameter for the Rayleigh damping."}>>> = 19.63
[../]
[./gravity]
type = Gravity<<<{"description": "Apply gravity. Value is in units of acceleration.", "href": "../../source/kernels/Gravity.html"}>>>
variable<<<{"description": "The name of the variable that this residual object operates on"}>>> = disp_y
value<<<{"description": "Value multiplied against the residual, e.g. gravitational acceleration"}>>> = -9.81
[../]
[]
[AuxKernels<<<{"href": "../../syntax/AuxKernels/index.html"}>>>]
[./accel_x] # Calculates and stores acceleration at the end of time step
type = NewmarkAccelAux<<<{"description": "Computes the current acceleration using the Newmark method.", "href": "../../source/auxkernels/NewmarkAccelAux.html"}>>>
variable<<<{"description": "The name of the variable that this object applies to"}>>> = accel_x
displacement<<<{"description": "displacement variable"}>>> = disp_x
velocity<<<{"description": "velocity variable"}>>> = vel_x
beta<<<{"description": "beta parameter for Newmark method"}>>> = 0.25
execute_on<<<{"description": "The list of flag(s) indicating when this object should be executed. For a description of each flag, see https://mooseframework.inl.gov/source/interfaces/SetupInterface.html."}>>> = timestep_end
[../]
[./vel_x] # Calculates and stores velocity at the end of the time step
type = NewmarkVelAux<<<{"description": "Calculates the current velocity using Newmark method.", "href": "../../source/auxkernels/NewmarkVelAux.html"}>>>
variable<<<{"description": "The name of the variable that this object applies to"}>>> = vel_x
acceleration<<<{"description": "acceleration variable"}>>> = accel_x
gamma<<<{"description": "gamma parameter for Newmark method"}>>> = 0.5
execute_on<<<{"description": "The list of flag(s) indicating when this object should be executed. For a description of each flag, see https://mooseframework.inl.gov/source/interfaces/SetupInterface.html."}>>> = timestep_end
[../]
[./accel_y]
type = NewmarkAccelAux<<<{"description": "Computes the current acceleration using the Newmark method.", "href": "../../source/auxkernels/NewmarkAccelAux.html"}>>>
variable<<<{"description": "The name of the variable that this object applies to"}>>> = accel_y
displacement<<<{"description": "displacement variable"}>>> = disp_y
velocity<<<{"description": "velocity variable"}>>> = vel_y
beta<<<{"description": "beta parameter for Newmark method"}>>> = 0.25
execute_on<<<{"description": "The list of flag(s) indicating when this object should be executed. For a description of each flag, see https://mooseframework.inl.gov/source/interfaces/SetupInterface.html."}>>> = timestep_end
[../]
[./vel_y]
type = NewmarkVelAux<<<{"description": "Calculates the current velocity using Newmark method.", "href": "../../source/auxkernels/NewmarkVelAux.html"}>>>
variable<<<{"description": "The name of the variable that this object applies to"}>>> = vel_y
acceleration<<<{"description": "acceleration variable"}>>> = accel_y
gamma<<<{"description": "gamma parameter for Newmark method"}>>> = 0.5
execute_on<<<{"description": "The list of flag(s) indicating when this object should be executed. For a description of each flag, see https://mooseframework.inl.gov/source/interfaces/SetupInterface.html."}>>> = timestep_end
[../]
[./accel_z]
type = NewmarkAccelAux<<<{"description": "Computes the current acceleration using the Newmark method.", "href": "../../source/auxkernels/NewmarkAccelAux.html"}>>>
variable<<<{"description": "The name of the variable that this object applies to"}>>> = accel_z
displacement<<<{"description": "displacement variable"}>>> = disp_z
velocity<<<{"description": "velocity variable"}>>> = vel_z
beta<<<{"description": "beta parameter for Newmark method"}>>> = 0.25
execute_on<<<{"description": "The list of flag(s) indicating when this object should be executed. For a description of each flag, see https://mooseframework.inl.gov/source/interfaces/SetupInterface.html."}>>> = timestep_end
[../]
[./vel_z]
type = NewmarkVelAux<<<{"description": "Calculates the current velocity using Newmark method.", "href": "../../source/auxkernels/NewmarkVelAux.html"}>>>
variable<<<{"description": "The name of the variable that this object applies to"}>>> = vel_z
acceleration<<<{"description": "acceleration variable"}>>> = accel_z
gamma<<<{"description": "gamma parameter for Newmark method"}>>> = 0.5
execute_on<<<{"description": "The list of flag(s) indicating when this object should be executed. For a description of each flag, see https://mooseframework.inl.gov/source/interfaces/SetupInterface.html."}>>> = timestep_end
[../]
[./stress_xx]
type = RankTwoAux<<<{"description": "Access a component of a RankTwoTensor", "href": "../../source/auxkernels/RankTwoAux.html"}>>>
rank_two_tensor<<<{"description": "The rank two material tensor name"}>>> = stress
variable<<<{"description": "The name of the variable that this object applies to"}>>> = stress_xx
index_i<<<{"description": "The index i of ij for the tensor to output (0, 1, 2)"}>>> = 0
index_j<<<{"description": "The index j of ij for the tensor to output (0, 1, 2)"}>>> = 0
[../]
[./strain_xx]
type = RankTwoAux<<<{"description": "Access a component of a RankTwoTensor", "href": "../../source/auxkernels/RankTwoAux.html"}>>>
rank_two_tensor<<<{"description": "The rank two material tensor name"}>>> = total_strain
variable<<<{"description": "The name of the variable that this object applies to"}>>> = strain_xx
index_i<<<{"description": "The index i of ij for the tensor to output (0, 1, 2)"}>>> = 0
index_j<<<{"description": "The index j of ij for the tensor to output (0, 1, 2)"}>>> = 0
[../]
[./stress_yy]
type = RankTwoAux<<<{"description": "Access a component of a RankTwoTensor", "href": "../../source/auxkernels/RankTwoAux.html"}>>>
rank_two_tensor<<<{"description": "The rank two material tensor name"}>>> = stress
variable<<<{"description": "The name of the variable that this object applies to"}>>> = stress_yy
index_i<<<{"description": "The index i of ij for the tensor to output (0, 1, 2)"}>>> = 1
index_j<<<{"description": "The index j of ij for the tensor to output (0, 1, 2)"}>>> = 1
[../]
[./strain_yy]
type = RankTwoAux<<<{"description": "Access a component of a RankTwoTensor", "href": "../../source/auxkernels/RankTwoAux.html"}>>>
rank_two_tensor<<<{"description": "The rank two material tensor name"}>>> = total_strain
variable<<<{"description": "The name of the variable that this object applies to"}>>> = strain_yy
index_i<<<{"description": "The index i of ij for the tensor to output (0, 1, 2)"}>>> = 1
index_j<<<{"description": "The index j of ij for the tensor to output (0, 1, 2)"}>>> = 1
[../]
[./stress_zz]
type = RankTwoAux<<<{"description": "Access a component of a RankTwoTensor", "href": "../../source/auxkernels/RankTwoAux.html"}>>>
rank_two_tensor<<<{"description": "The rank two material tensor name"}>>> = stress
variable<<<{"description": "The name of the variable that this object applies to"}>>> = stress_zz
index_i<<<{"description": "The index i of ij for the tensor to output (0, 1, 2)"}>>> = 2
index_j<<<{"description": "The index j of ij for the tensor to output (0, 1, 2)"}>>> = 2
[../]
[./strain_zz]
type = RankTwoAux<<<{"description": "Access a component of a RankTwoTensor", "href": "../../source/auxkernels/RankTwoAux.html"}>>>
rank_two_tensor<<<{"description": "The rank two material tensor name"}>>> = total_strain
variable<<<{"description": "The name of the variable that this object applies to"}>>> = strain_zz
index_i<<<{"description": "The index i of ij for the tensor to output (0, 1, 2)"}>>> = 2
index_j<<<{"description": "The index j of ij for the tensor to output (0, 1, 2)"}>>> = 2
[../]
[]
[Functions<<<{"href": "../../syntax/Functions/index.html"}>>>]
[./displacement_front]
type = PiecewiseLinear<<<{"description": "Linearly interpolates between pairs of x-y data", "href": "../../source/functions/PiecewiseLinear.html"}>>>
data_file<<<{"description": "File holding CSV data"}>>> = 'displacement.csv'
format<<<{"description": "Format of csv data file that is in either in columns or rows"}>>> = columns
[../]
[]
[BCs<<<{"href": "../../syntax/BCs/index.html"}>>>]
[./prescribed_displacement]
type = PresetDisplacement<<<{"description": "Prescribe the displacement on a given boundary in a given direction.", "href": "../../source/bcs/PresetDisplacement.html"}>>>
variable<<<{"description": "The name of the variable that this residual object operates on"}>>> = disp_z
velocity<<<{"description": "The velocity variable."}>>> = vel_z
acceleration<<<{"description": "The acceleration variable."}>>> = accel_z
beta<<<{"description": "beta parameter for Newmark time integration."}>>> = 0.25
boundary<<<{"description": "The list of boundary IDs from the mesh where this object applies"}>>> = front
function<<<{"description": "Function describing the displacement."}>>> = displacement_front
[../]
[./anchor_x]
type = DirichletBC<<<{"description": "Imposes the essential boundary condition $u=g$, where $g$ is a constant, controllable value.", "href": "../../source/bcs/DirichletBC.html"}>>>
variable<<<{"description": "The name of the variable that this residual object operates on"}>>> = disp_x
boundary<<<{"description": "The list of boundary IDs from the mesh where this object applies"}>>> = left
value<<<{"description": "Value of the BC"}>>> = 0.0
[../]
[./anchor_y]
type = DirichletBC<<<{"description": "Imposes the essential boundary condition $u=g$, where $g$ is a constant, controllable value.", "href": "../../source/bcs/DirichletBC.html"}>>>
variable<<<{"description": "The name of the variable that this residual object operates on"}>>> = disp_y
boundary<<<{"description": "The list of boundary IDs from the mesh where this object applies"}>>> = bottom
value<<<{"description": "Value of the BC"}>>> = 0.0
[../]
[./anchor_z]
type = DirichletBC<<<{"description": "Imposes the essential boundary condition $u=g$, where $g$ is a constant, controllable value.", "href": "../../source/bcs/DirichletBC.html"}>>>
variable<<<{"description": "The name of the variable that this residual object operates on"}>>> = disp_z
boundary<<<{"description": "The list of boundary IDs from the mesh where this object applies"}>>> = back
value<<<{"description": "Value of the BC"}>>> = 0.0
[../]
[]
[Materials<<<{"href": "../../syntax/Materials/index.html"}>>>]
[./elasticity_tensor]
youngs_modulus<<<{"description": "Young's modulus of the material."}>>> = 325e6 #Pa
poissons_ratio<<<{"description": "Poisson's ratio for the material."}>>> = 0.3
type = ComputeIsotropicElasticityTensor<<<{"description": "Compute a constant isotropic elasticity tensor.", "href": "../../source/materials/ComputeIsotropicElasticityTensor.html"}>>>
block<<<{"description": "The list of blocks (ids or names) that this object will be applied"}>>> = 0
[../]
[./strain]
#Computes the strain, assuming small strains
type = ComputeSmallStrain<<<{"description": "Compute a small strain.", "href": "../../source/materials/ComputeSmallStrain.html"}>>>
block<<<{"description": "The list of blocks (ids or names) that this object will be applied"}>>> = 0
displacements<<<{"description": "The displacements appropriate for the simulation geometry and coordinate system"}>>> = 'disp_x disp_y disp_z'
[../]
[./stress]
#Computes the stress, using linear elasticity
type = ComputeLinearElasticStress<<<{"description": "Compute stress using elasticity for small strains", "href": "../../source/materials/ComputeLinearElasticStress.html"}>>>
block<<<{"description": "The list of blocks (ids or names) that this object will be applied"}>>> = 0
[../]
[./density]
type = GenericConstantMaterial<<<{"description": "Declares material properties based on names and values prescribed by input parameters.", "href": "../../source/materials/GenericConstantMaterial.html"}>>>
block<<<{"description": "The list of blocks (ids or names) that this object will be applied"}>>> = 0
prop_names<<<{"description": "The names of the properties this material will have"}>>> = density
prop_values<<<{"description": "The values associated with the named properties"}>>> = 2000 #kg/m3
[../]
[]
[Controls<<<{"href": "../../syntax/Controls/index.html"}>>>] # turns off inertial terms for the first time step
[./period0]
type = TimePeriod<<<{"description": "Control the enabled/disabled state of objects with time.", "href": "../../source/controls/TimePeriod.html"}>>>
disable_objects<<<{"description": "A list of object tags to disable."}>>> = '*/vel_x */vel_y */vel_z */accel_x */accel_y */accel_z */inertia_x */inertia_y */inertia_z'
start_time<<<{"description": "The time at which the objects are to be enabled/disabled."}>>> = 0.0
end_time<<<{"description": "The time at which the objects are to be enable/disabled."}>>> = 0.1 # dt used in the simulation
[../]
[../]
[Executioner<<<{"href": "../../syntax/Executioner/index.html"}>>>]
type = Transient
start_time = 0
end_time = 3.0
l_tol = 1e-6
nl_rel_tol = 1e-6
nl_abs_tol = 1e-6
dt = 0.1
timestep_tolerance = 1e-6
[]
[Postprocessors<<<{"href": "../../syntax/Postprocessors/index.html"}>>>] # These quantites are printed to a csv file at every time step
[./_dt]
type = TimestepSize<<<{"description": "Reports the timestep size", "href": "../../source/postprocessors/TimestepSize.html"}>>>
[../]
[./accel_6x]
type = NodalVariableValue<<<{"description": "Outputs values of a nodal variable at a particular location", "href": "../../source/postprocessors/NodalVariableValue.html"}>>>
nodeid<<<{"description": "The ID of the node where we monitor"}>>> = 6
variable<<<{"description": "The variable to be monitored"}>>> = accel_x
[../]
[./accel_6y]
type = NodalVariableValue<<<{"description": "Outputs values of a nodal variable at a particular location", "href": "../../source/postprocessors/NodalVariableValue.html"}>>>
nodeid<<<{"description": "The ID of the node where we monitor"}>>> = 6
variable<<<{"description": "The variable to be monitored"}>>> = accel_y
[../]
[./accel_6z]
type = NodalVariableValue<<<{"description": "Outputs values of a nodal variable at a particular location", "href": "../../source/postprocessors/NodalVariableValue.html"}>>>
nodeid<<<{"description": "The ID of the node where we monitor"}>>> = 6
variable<<<{"description": "The variable to be monitored"}>>> = accel_z
[../]
[./vel_6x]
type = NodalVariableValue<<<{"description": "Outputs values of a nodal variable at a particular location", "href": "../../source/postprocessors/NodalVariableValue.html"}>>>
nodeid<<<{"description": "The ID of the node where we monitor"}>>> = 6
variable<<<{"description": "The variable to be monitored"}>>> = vel_x
[../]
[./vel_6y]
type = NodalVariableValue<<<{"description": "Outputs values of a nodal variable at a particular location", "href": "../../source/postprocessors/NodalVariableValue.html"}>>>
nodeid<<<{"description": "The ID of the node where we monitor"}>>> = 6
variable<<<{"description": "The variable to be monitored"}>>> = vel_y
[../]
[./vel_6z]
type = NodalVariableValue<<<{"description": "Outputs values of a nodal variable at a particular location", "href": "../../source/postprocessors/NodalVariableValue.html"}>>>
nodeid<<<{"description": "The ID of the node where we monitor"}>>> = 6
variable<<<{"description": "The variable to be monitored"}>>> = vel_z
[../]
[./disp_6x]
type = NodalVariableValue<<<{"description": "Outputs values of a nodal variable at a particular location", "href": "../../source/postprocessors/NodalVariableValue.html"}>>>
nodeid<<<{"description": "The ID of the node where we monitor"}>>> = 6
variable<<<{"description": "The variable to be monitored"}>>> = disp_x
[../]
[./disp_6y]
type = NodalVariableValue<<<{"description": "Outputs values of a nodal variable at a particular location", "href": "../../source/postprocessors/NodalVariableValue.html"}>>>
nodeid<<<{"description": "The ID of the node where we monitor"}>>> = 6
variable<<<{"description": "The variable to be monitored"}>>> = disp_y
[../]
[./disp_6z]
type = NodalVariableValue<<<{"description": "Outputs values of a nodal variable at a particular location", "href": "../../source/postprocessors/NodalVariableValue.html"}>>>
nodeid<<<{"description": "The ID of the node where we monitor"}>>> = 6
variable<<<{"description": "The variable to be monitored"}>>> = disp_z
[../]
[]
[Outputs<<<{"href": "../../syntax/Outputs/index.html"}>>>]
exodus<<<{"description": "Output the results using the default settings for Exodus output."}>>> = true
perf_graph<<<{"description": "Enable printing of the performance graph to the screen (Console)"}>>> = true
[]