Solid Mechanics Module
The Solid Mechanics module is a library of simulation tools that solve continuum mechanics problems. It provides a simple approach for implementing even advanced mechanics models:
Plug-n-play design enables users to incorporate the relevant physics for specific and varied simulations
Tensor implementation matches mathematical theory
Straight-forward procedure for adding new physics
The solid mechanics system can be used to simulate both linear and finite strain mechanics, including Elasticity and Cosserat elasticity, Plasticity and micromechanics plasticity, Creep, and Damage due to cracking and property degradation
Explore the Capabilities and Start Modeling
The Solid Mechanics module is used in a variety of pure mechanics simulations and in combined physics simulations with the Heat Transfer, Phase Field, Contact, Porous Flow, and XFEM modules; use the MOOSE combined module to perform simulations with multiple physics modules. The following figures show results from a few different simulations performed by solid mechanics module users.
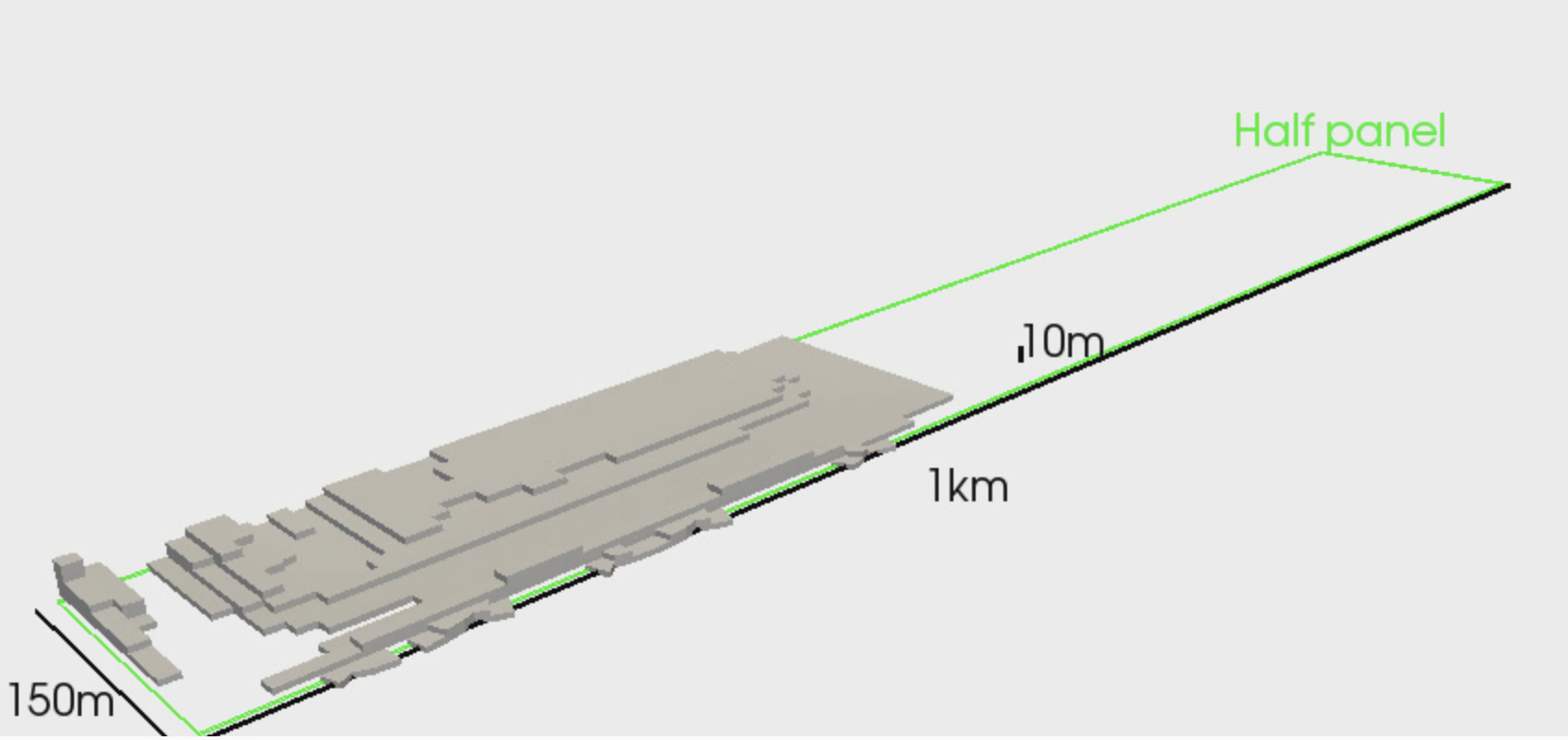
Evolution of rock failure zone in a 300m-wide, 400m-deep panel in a coal mining application.
Evolution of the resolved shear stress on the slip system in a polycrystalline simulation of BCC Iron.
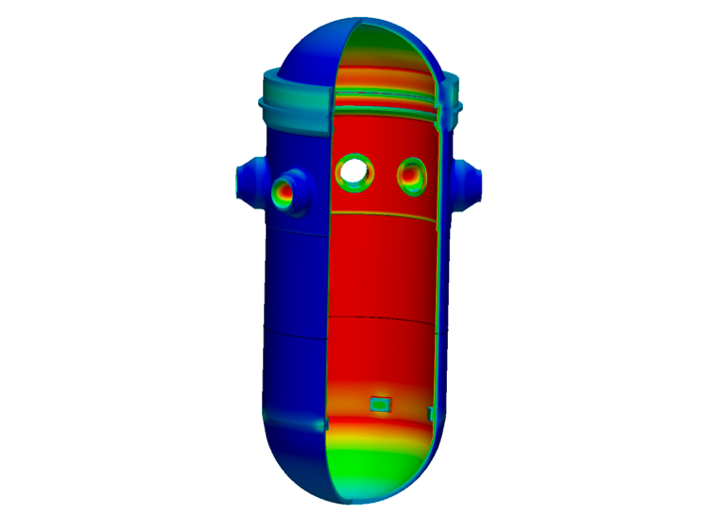
Thermo-mechanical stress analysis of a reactor pressure vessel.
Interested in performing some of these simulations yourself? Use the links below to learn more about the solid mechanics module and to get started with your own continuum mechanics and combined physics simulations.
Plug-n-Play Structure Overview
Familiarize yourself with the Plug-n-Play Structure used by solid mechanics and then dive into the mathematical theory:
These types of code classes make up the core of the solid mechanics module.
Examples and Tutorials
Get started running your own solid mechanics simulations by exploring the introductory tutorials and examples. Next browse through the information:
Now you're ready to start creating your own mechanics simulations.
Advanced Features
Explore the different ways to use the solid mechanics module by browsing the introductory theory pages on the various models:
New Mechanics Kernels
The Solid Mechanics module currently has two, partially interoperable underlying systems:
The current system based on the StressDivergenceTensors and related kernels.
A newer system based on the TotalLagrangianStressDivergence and UpdatedLagrangianStressDivergence kernels.
The current system may suffer from convergence issues caused by non-exact Jacobians for large deformations problems when not used with the Automatic Differentiation variants of the kernels and underlying materials. The newer system (referred to in the documentation as the Lagrangian kernels) has exact Jacobians and also includes:
A common interface for running small or large deformation problems that simplifies how input files are setup and makes it easier to switch between different kinematic and material models.
An improved material system, that provides multiple options for implementing new materials models. The new material system can also automatically convert a small deformation material model to large deformation kinematics by integrating a user-select objective stress rate.
Both total Lagrangian and updated Lagrangian formulations.
A homogenization system designed to enforce cell-average deformation or stress conditions over a periodic unit cell.
Stabilization for linear elements for use in incompressible or nearly-incompressible problems through a formulation.
The newer kernels are compatible with the existing MOOSE materials via the ComputeLagrangianWrappedStress object. This object maps the output from the existing MOOSE material system into the format expected by the Lagrangian kernels.
The Lagrangian kernels are feature-complete with the original kernels – all simulations using the original kernels should be able to be converted to use the Lagrangian kernels. However, users should be aware that modules that couple to "stress" for the Cauchy stress using the original kernels should now either couple to "cauchy_stress" or "pk1_stress", as appropriate, in the Lagrangian kernels.
Users should consider using the new system for problems where numerical convergence is critical – for example problems with large material or geometric nonlinearities – or for problems where the stress update provided by the constitutive model is very expensive, as the new kernels will achieve convergence in many fewer nonlinear iterations, when compared to the older system.
Both the new and old systems are accessible through the SolidMechanics/QuasiStatic, which simplifies the process of setting up and running models.
Developing New Solid Mechanics Code
The SolidMechanics module is being developed by users at national laboratories and universities around the world. Learn how to get in touch with the developers on the help/contact_us.md page.
Consider becoming a developer yourself. The solid mechanics module uses code syntax based on tensor forms. This approach allows the constitutive tensor equations to be implemented, clearly and concisely, in the same format as written in mathematical notation. Follow the MOOSE standards for contributing.
Software Quality
The Solid Mechanics module follows strict software quality guidelines, refer to Solid Mechanics SQA for more information.